Одинаковые ли пути проходят правые и левые колеса: 105. Одинаковые ли пути проходят правые и левые колеса автомобиля при повороте (рис. 23)?

Содержание

№ 105 Сборник задач по физике 7-9 класс Лукашик. Одинаковые ли пути проходят правые и левые колеса автомобиля – Рамблер/класс

№ 105 Сборник задач по физике 7-9 класс Лукашик. Одинаковые ли пути проходят правые и левые колеса автомобиля – Рамблер/класс

Интересные вопросы

Школа

Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?

Новости

Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?

Школа

Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?

Школа

Когда в 2018 году намечено проведение основного периода ЕГЭ?

Новости

Будет ли как-то улучшаться система проверки и организации итоговых сочинений?

Вузы

Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?

Одинаковые ли пути проходят правые и левые колеса автомобиля при повороте (рис.

23)?

ответы

Нет, меньшее расстояние проходят колеса, в сторону которых происходит поворот.

ваш ответ

Можно ввести 4000 cимволов

отправить

дежурный

Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения

похожие темы

Экскурсии

Мякишев Г.Я.

Психология

Химия

похожие вопросы 5

№ 179 Сборник задач по физике 7-9 класс Лукашик. Почему патрон продолжает вращаться?

У кого есть ответ?
Почему после выключения двигателя сверлильного станка патрон продолжает вращаться?

ГДЗФизика7 класс8 класс9 классЛукашик В.И.

Приготовление раствора сахара и расчёт его массовой доли в растворе. Химия. 8 класс. Габриелян. ГДЗ. Хим. практикум № 1. Практ. работа № 5.

Попробуйте провести следующий опыт. Приготовление раствора
сахара и расчёт его массовой доли в растворе.
Отмерьте мерным (Подробнее…)

ГДЗШкола8 классХимияГабриелян О.С.

ГДЗ Тема 21 Физика 7-9 класс А.В.Перышкин Задание №475 В обоих случаях поплавок плавает. В какую жидкость он погружается глубже?

Привет. Выручайте с ответом по физике…
Поплавок со свинцовым грузилом внизу опускают
сначала в воду, потом в масло. В обоих (Подробнее…)

ГДЗФизикаПерышкин А.В.Школа7 класс

ГДЗ Тема 21 Физика 7-9 класс А.В.Перышкин Задание №476 Изобразите силы, действующие на тело.

Привет всем! Нужен ваш совет, как отвечать…
Изобразите силы, действующие на тело, когда оно плавает на поверхности жидкости. (Подробнее…)

ГДЗФизикаПерышкин А.В.Школа7 класс

Ребята нужны ответы на пересдачу по математике 9 класс 11 регион. Срочно!

ГИА9 класс

Геометрия поворота / Этюды // Математические этюды

Математические этюды

К списку

Параллельны ли друг другу передние колёса автомобиля при повороте?

Оказывается, что именно геометрия и механика определяют то, как надо поворачивать колёса автомобиля.

Если продолжение оси колёс направлено в центр поворота, то колесо оставляет чёткий след. Чёткая картинка будет, и если несколько осей направлены в центр поворота. Однако, если продолжение оси колеса направлено не в центр поворота, то колесо катится с проскальзыванием. След будет стёртым, а самое главное, управляемость транспорта с таким колесом будет тем хуже, чем выше скорость. Итак, для хорошей управляемости продолжения осей колес должны быть направлены в центр поворота. Что же это значит для четырёхколёсного автомобиля?

Научимся для начала проходить простой поворот — дугу окружности.

Так как задние колёса в большинстве машин не поворачиваются, то центр окружности поворота должен лежать на продолжении оси этих колёс. Передние колёса необходимо повернуть так, чтобы продолжение оси каждого колеса смотрело в этот же центр. А значит, для хорошей управляемости передние колёса необходимо поворачивать на разные углы, и они будут непараллельны!

Вы скажете, что повороты не всегда являются дугой какой-либо окружности, и уж тем более машина не останавливается для того, чтобы повернуть колёса. Это, конечно, правда, но оказывается, что при любом повороте в каждый момент времени можно считать, что машина едет по дуге некоторой окружности (радиус и центр которой зависят от момента времени).

Рассмотрим произвольную дорогу. Чтобы по ней можно было ездить, у неё не должно быть острых углов, т.е. средняя линия будет, как говорят в математике, гладкой кривой.

Зафиксируем синюю точку на средней линии и подумаем, каким более простым геометрическим объектом можно заменить кривую в небольшой окрестности нашей точки.

Возьмём произвольную красную точку недалеко от синей. Две точки на плоскости определяют единственную прямую, которую и проведём. Будем двигать красную точку по кривой к синей. В момент, когда они совпадут, прямая, ими определяемая, будет касательной прямой. Она даёт линейное приближение кривой дороги в небольшой окрестности зафиксированной точки. Однако при увеличении видно, что дорога и касательная прямая рядом идут на очень маленьком участке.

Справа и слева от синей точки возьмём по красной. Три точки, не лежащие на одной прямой, определяют единственную окружность, которую и проведём. Будем двигать красные точки к синей. В момент, когда они совпадут, получим окружность, которая называется соприкасающейся. Это приближение уже второго порядка, и на увеличении видно, насколько оно лучше. Заметим, что на монотонном участке (возрастания или убывания кривой) соприкасающаяся окружность всегда пересекает кривую, в отличие от касательной, расположенной на таких участках по одну сторону от кривой.

Так как соприкасающаяся окружность для нашей задачи хорошо приближает дорогу и может быть построена в любой её точке, то движение по изгибам дороги можно рассматривать в каждый момент времени как движение по дуге некоторой окружности. Мгновенные радиус и центр этой окружности зависят, конечно, от той точки, в которой находится машина.

Таким образом, при движении в произвольном повороте можно считать, что в каждый момент времени машина движется по небольшой дуге некоторой окружности. И наш первый случай — поворот машины по дуге окружности — основной, который и нужно изучать.

Но как достичь того, чтобы при любом повороте колёс продолжение осей смотрело в мгновенный центр поворота?

Оказывается, и здесь на помощь приходит геометрия, а именно известная со школы равнобокая трапеция — четырёхугольник, у которого две стороны, называемые основаниями, параллельны между собой, а боковые стороны равны друг другу. Если правильно подобрать размеры сторон трапеции, то достигается небоходимое для хорошего управления условие — продолжение осей передних колёс пересекается в точке, лежащей на продолжении оси задних колёс. Эта точка и есть мгновенный центр поворота машины.

Придумал такое управление передними колёсами француз, каретных дел мастер Шарль Жанто (Charles Jeantand).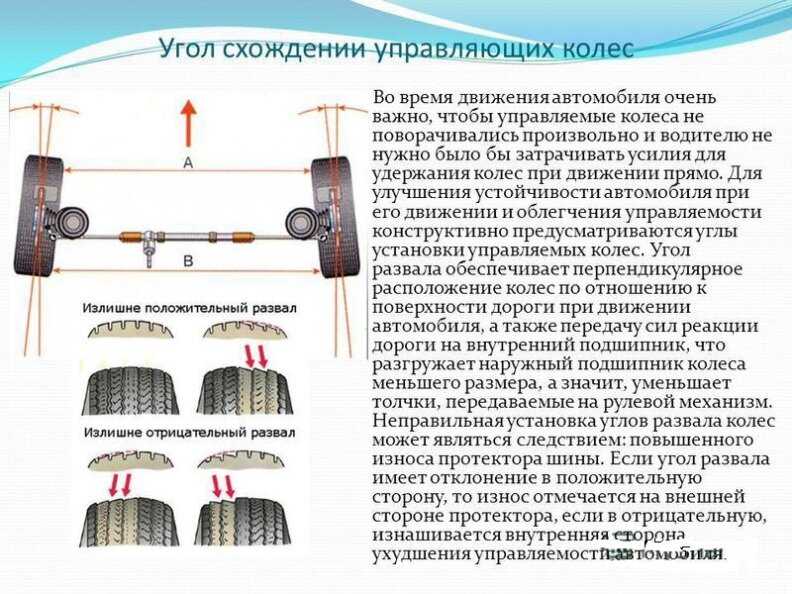 Однако для карет, передвигавшихся с малыми скоростями, это было не так существенно, как для машин, и изобретение Жанто было забыто. Лишь почти через три четверти века два отца автомобилестроения, два немца, два инженера — Готтлиб Даймлер (Gottlieb Wilhelm Daimler) и Карл Бенц (Karl Friedrich Michael Benz) — изобретая свои автомобили, возвращаются к трапеции Жанто. В 1889 году Даймлер получает патент на «способ независимого управления передними колёсами с разновеликими радиусами поворота». А в 1893 году Бенц получает патент на «устройство управления экипажей с тангенциальными к колёсам окружностями управления». Решив задачу управления передними поворотными колёсами и другие важные технические вопросы, Карл Бенц строит свой первый знаменитый четырёхколёсный автомобиль «Виктория».

С точки зрения строгой математики, трапеция не позволяет достичь необходимого условия — чтобы продолжение осей передних колес при любом повороте пересекалось в точке, лежащей на продолжении задней оси.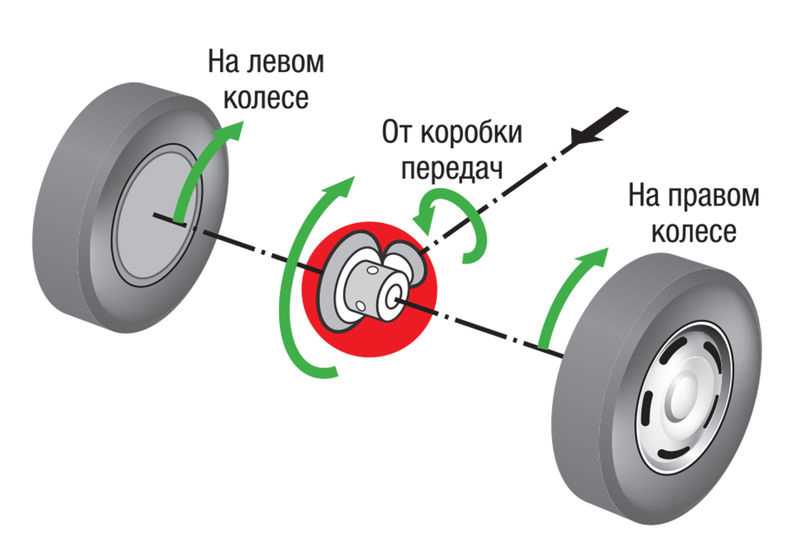

При использовании трапеции эта точка будет всегда лежать чуть-чуть в стороне от линии задней оси. Зачем же мы столько обсуждали трапецию, скажете вы? Расстраиваться рано — просто не надо бездумно переносить математическую строгость в технические вопросы. Чтобы точка пересечения линий передних осей всегда лежала на линии задней оси, необходимо, чтобы длина меньшего основания трапеции немного менялась. При общей длине этого основания более метра необходимые изменения длины составляют всего около одного сантиметра, а это меньше чем люфты в соединениях и разрешённые допуски при изготовлении.

Со времён изобретения первых автомобилей скорости передвижения сильно возросли. Увеличились и требования к управлению передними колёсами. Кроме того, трапеция — это плоская геометрическая фигура. И такой способ управления передними колёсами может использоваться только при зависимой передней подвеске — когда колёса жёстко связаны друг с другом и прямая, соединяющая их центры, всегда параллельна плоскости трапеции. Сейчас такое можно встретить на грузовых автомобилях. На современных легковых автомобилях подвеска колёс независима, т.е. они могут ходить по высоте друг относительно друга. Для управления в повороте такими колёсами применяются более сложные, уже неплоские шарнирные механизмы, чаще всего с центральным звеном в виде рулевой рейки. Но их расчёт — это тоже задача математиков и механиков. А исторически они так по-прежнему и называются — рулевой трапецией.

При повороте автомобиля возникает ещё один вопрос, связанный с геометрией. Длина окружности радиуса R равна, как вы помните, 2πR. Соответственно, длина дуги, опирающейся на угол α окружности радиуса R, равна αR. При повороте автомобиля по дуге окружности внешнее переднее колесо едет по дуге окружности большего радиуса, чем внутреннее переднее. Точно так же и заднее внешнее колесо описывает дугу большего радиуса, чем внутреннее заднее. А раз радиусы различаются, то, значит, пути, проходимые внутренним и внешним колёсами одной оси, должны быть тоже различны. В противном случае колесо будет проскальзывать, и управляемость автомобиля снизится.

В случае, когда ось неведущая, т.е. её колёса не толкают автомобиль вперёд, всё просто: каждое колесо вертится со своей скоростью, необходимой для прохождения нужного пути без проскальзывания.

А как же сделать так, чтобы колёса ведущей оси, в нашем случае задней, с одной стороны, постоянно толкали автомобиль вперёд, а с другой стороны, могли вращаться с разными скоростями?

Помогает в этом дифференциал — представитель планетарных механизмов. Планетарным называется механизм, у которого есть сателлиты — шестерни, крутящиеся вокруг подвижных осей.

Вал от мотора, пройдя через коробку передач, отдаёт вращение на «бочку». Бочка же через сателлиты передаёт вращение на левую и правую полуоси ведущей оси.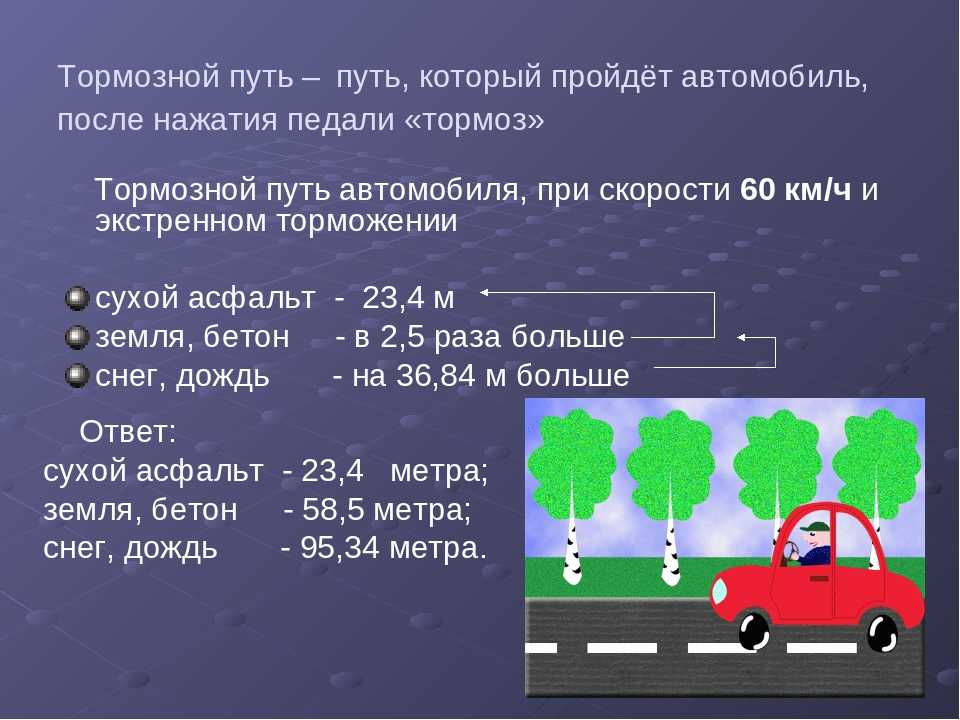 Как бы ни вращались колёса, скорость бочки всегда в два раза медленнее вращения вала, а сумма скоростей полуосей равна удвоенной скорости вала.

Если машина едет по прямой и под обоими ведущими колёсами одинаковое покрытие — с одинаковым коэффициентом трения, то колёса забирают от бочки одинаковое количество вращения, и полуоси вращаются (колёса и их полуоси) с одинаковой скоростью.

Но если коэффициенты трения различаются, например, одна сторона машины выезжает с асфальта на грунтовую обочину или попадает на лёд, то… Как же будут себя вести колёса при прохождении этого участка? У колёс неведущей оси всё просто: они независимы друг от друга, им не надо толкать машину, и когда одно из них выкатывается на лёд, то перестаёт крутиться, так как трение с дорогой очень маленькое.

Вот и под левое колесо ведущей оси попадает лёд. Справа трение с асфальтом большое, а слева — со льдом — почти отсутствует.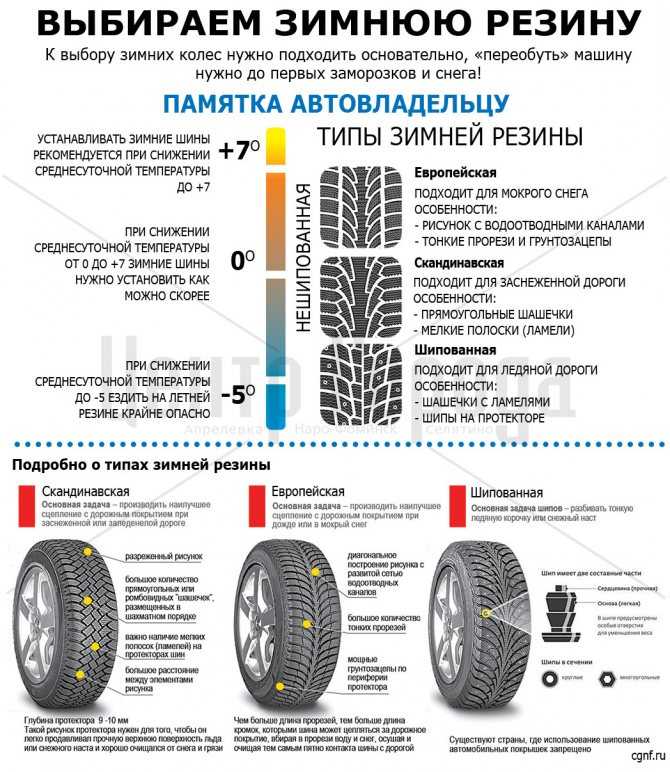 Соответственно, левому колесу вращаться гораздо проще, и оно начинает забирать на себя всё вращение, отдаваемое бочкой на обе полуоси. При этом сумма скоростей полуосей, как было отмечено выше, всегда постоянна, но одна полуось не крутится, а вторая — вращается очень быстро. Начать движение из такого положения, когда одно колесо ведущей оси потеряло связь с дорогой (например, находится на льду), а другое нет — невозможно.

Казалось бы, одни неудобства от этого дифференциала, зачем он тогда нужен? Как раз для решения задачи одновременного толкания ведущей осью машины вперёд и прохождения в поворотах ведущими колесами путей разной длины. Каждое колесо берёт от дифференциала количество движения пропорционально длине его пути, а в сумме всю энергию вала они затрачивают на движение машины вперёд.

Инженеры постоянно пытаются улучшить дифференциал, сохранив его основное свойство, пытаются уменьшить неприятные эффекты — каким-либо способом не давать крутиться полуосям со слишком большой разницей скоростей.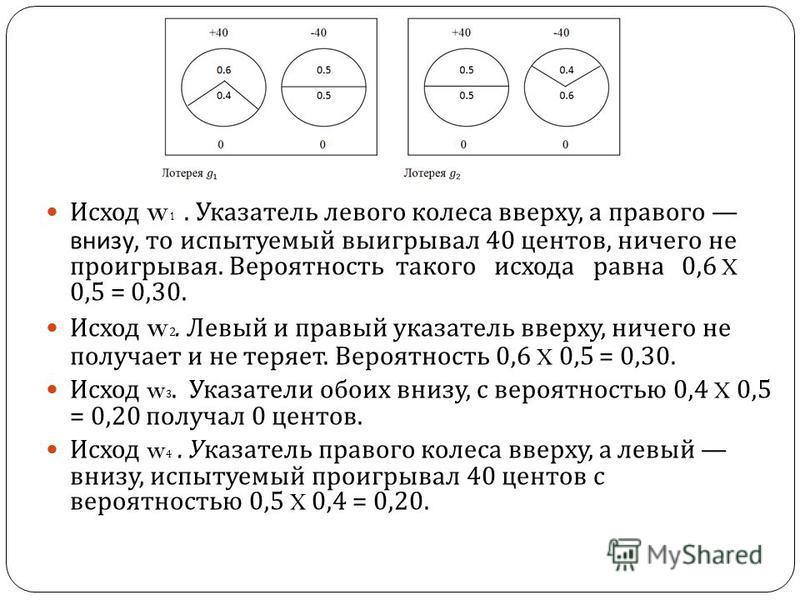 Но по сути, всё и сегодня остаётся таким же, ибо законы геометрии никто не отменял.

Смотри также

Поворот передних колёс автомобиля // Математическая составляющая / Ред.-сост. Н. Н. Андреев, С. П. Коновалов, Н. М. Панюнин. — Второе издание, расширенное и дополненное. — М. : Математические этюды, 2019. — С. 54—55, 306.

Млодзеевский Б. К. К теории управления в автомобилях // Вестник инженеров. 1917. 15 января. Т. 3, № 2. С. 37—41.

Другие этюды раздела «Математика и техника»

Колёсная пара Уголковый отражатель Глубина заложения

Математические этюды

повседневная жизнь — Во время поворота задние колеса обязательно описывают те же дуги, что и передние колеса?

спросил 7 лет, 7 месяцев назад

Изменено 1 месяц назад

Просмотрено 8к раз

$\begingroup$

Когда автомобиль делает поворот, два передних колеса описывают две дуги, как показано на рисунке ниже. Колесо, обращенное внутрь поворота, имеет угол поворота больше, чем у внешнего колеса. Это необходимо для того, чтобы оба передних колеса плавно описывали две дуги, имеющие один и тот же центр, иначе при повороте передние колеса будут скользить по земле.

Во время поворота задние колеса обязательно описывают те же дуги, что и передние колеса?

повседневная жизнь
динамика вращения

$\endgroup$

$\begingroup$

Нет, вообще нет. Вы можете понять это из геометрии рулевого управления Аккермана, описанной на моем сайте в статье «Параллельная парковка автомобиля».

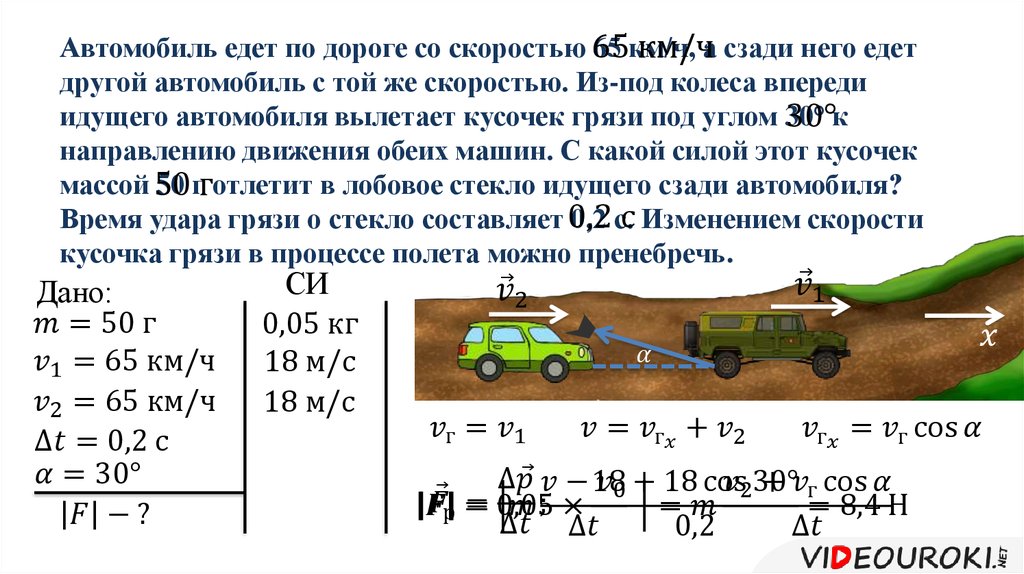
Подводя итог: посмотрите на определяющую геометрию для рулевого управления Аккермана, которую я набросал ниже:

Рулевое управление Аккермана определяется пересечением нормалей центрального блока ко всем колесам (осям вращательной симметрии) в общей точке $ C$ на схеме.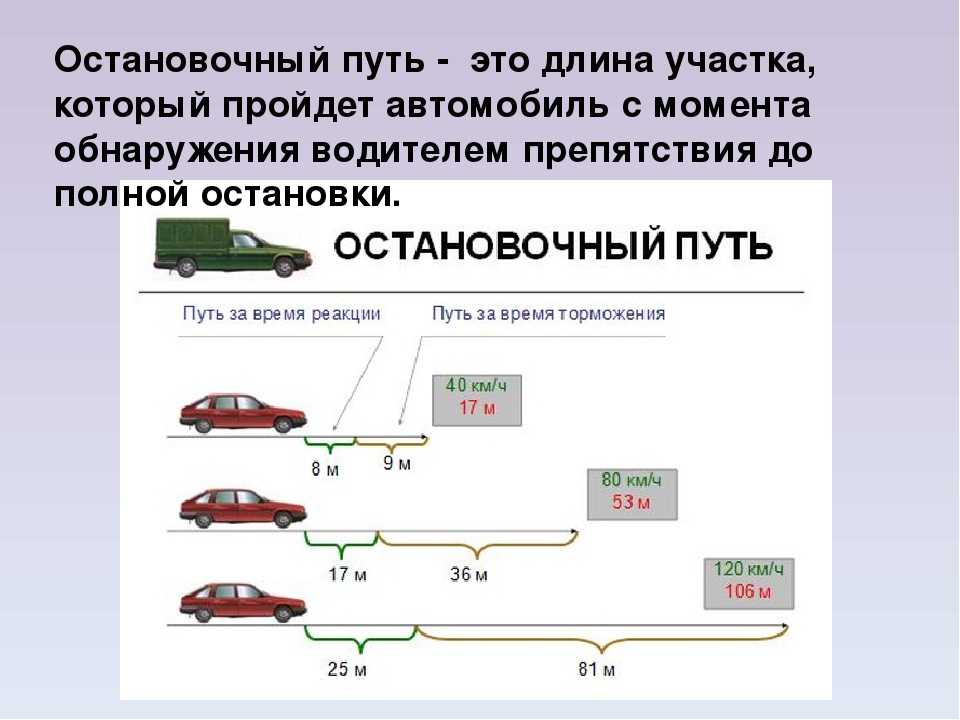 Таким образом, из диаграммы должно быть очень ясно, что радиус кривизны для каждого колеса разный: радиусы кривизны для дорожек передних колес немного больше, чем для дорожек задних колес. 9+(2)$- т. е. любое одновременное перемещение и плоскостное ориентационное вращение может быть реализовано как конечная последовательность операций управления.

Реальные автомобили всегда, пусть и незначительно, отклоняются от условия Аккермана. Действительно, если покрышка имеет ненулевую ширину, то какая-то ее часть должна либо циклически деформироваться при прохождении через точку контакта с землей, либо практически всегда присутствует некоторая пробуксовка, которую можно услышать, если очень медленно ехать на машине по трассе. полированной бетонной поверхности (например, на крытой парковке) и откройте окно.

$\endgroup$

$\begingroup$

Конечно нет. Задние колеса следуют траектории передних колес только тогда, когда автомобиль движется прямолинейно.

На повороте все совсем иначе. Задние колеса имеют тенденцию догонять передние по более короткому пути. Они как бы «срезают угол», при этом задняя часть автомобиля смещается ближе к центру поворота.

$\endgroup$

$\begingroup$

Это частая причина несчастных случаев, которых они не делают.

Если вы поворачиваете на крутом повороте (хорошим примером может быть поворот на узкую парковочную площадку рядом со столбом на автостоянке), любой опытный водитель знает, что перед поворотом нужно дать передним колесам почти выровняться с центром так сильно, как вы можете. Если вы сделаете широкий поворот и предполагаете, что задние колеса будут следовать за передними, вы поцарапаете боковую часть автомобиля о стойку (или что-то еще внутри поворота), как, я уверен, сделали многие люди.

$\endgroup$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

Геометрия рулевого управления / Этюды // Математические этюды

Эта система управления была изобретена французским мастером Шарлем Жантландом, который применил ее к передним колесам тележек. Но для телег, движущихся с малыми скоростями, это изобретение было не столь необходимо, как для автомобилей, и было забыто. Только спустя три четверти века два немецких инженера, два отца автомобиля, Готлиб Даймлер и Вильгельм Карл Фридрих Михаэль Бенц, строя свои автомобили, вернулись к джентландской трапеции. Даймлер в 1889 году получил патент на свой «способ независимого управления передними колесами с различными радиусами кривизны». И в1893 Бенц получил патент на свою «конструкцию системы управления с кругами управления, касательными к колесам». Решив проблему управления передними рулями и другие важные технические вопросы, Карл Бенц построил свой знаменитый автомобиль «Виктория» с четырьмя независимыми колесами.

С математической точки зрения трапеция не позволяет создать условия, необходимые для того, чтобы точка пересечения продолжений осей передних колес всегда лежала на продолжении оси задних колес. Используя трапецию, эта точка будет находиться немного дальше от линии задней оси. Но почему мы так долго говорили о трапеции, спросите вы? Мы слишком рано забеспокоились: мы просто не должны применять математическую строгость к техническим задачам, не руководствуясь здравым смыслом. Для того чтобы продолжения осей передних колес всегда пересекались в точке продолжения оси задних колес, необходимо, чтобы длина меньшего основания трапеции немного менялась. Для обычной длины его основания, которая составляет более одного метра, необходимые изменения будут состоять из длины в сантиметр, которая меньше промежутков между стыками, и допусков при изготовлении.

Со времени создания первой машины скорость резко возросла. Так же возросла потребность в лучшем контроле передних колес. Кроме того, трапеция представляет собой плоскую геометрическую фигуру: такой способ управления передними колесами можно использовать только при независимой передней подвеске, т. е. когда колеса жестко связаны друг с другом и прямая, соединяющая их центры, всегда параллельно плоскости трапеции.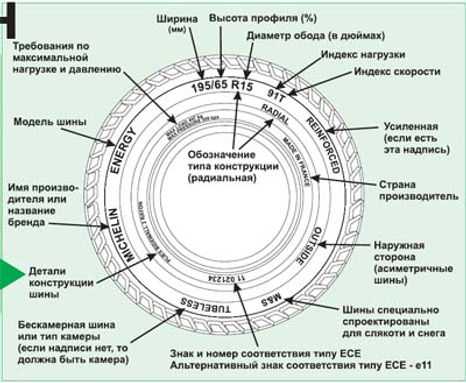 Теперь эту систему можно встретить и в грузовиках. В современных автомобилях подвески колес независимые, колеса могут двигаться в вертикальном направлении относительно друг друга. Для управления поворотом этих колес используются более сложные механизмы, уже не плоскостные, часто с центральным элементом, имеющим форму рейки. Даже в этом случае математикам и инженерам сложно рассчитать различные элементы. Но по историческим причинам эти механизмы продолжают называть рулевыми трапециями.

С рулевым управлением автомобиля возникает еще один вопрос, все же связанный с геометрией. Длина окружности радиуса R равна, как вы помните, 2R, а длина дуги амплитуды  равна  R. Когда автомобиль движется по дуге окружности, внешнее переднее колесо , наиболее удаленный от центра кривизны, движется по дуге радиуса больше, чем внутренняя часть. То же самое относится и к задним колесам: внешнее колесо описывает дугу большей длины, чем внутреннее колесо. А так как лучи разные, то и длины путей колес, соединенных одной осью, должны быть разными. В обратном случае одно из двух колес должно скользить, и это должно снизить управляемость автомобиля.

В случае, когда ось колес не является основной, т. е. колеса не ведущие — в нашем случае передние колеса — все просто: каждое колесо поворачивается со своей скоростью, необходимой для прохождения нужного поворота без заноса .

Но как сделать так, чтобы ведущие колеса — в нашем случае задние колеса — с одной стороны постоянно двигали машину вперед, а с другой вращались с разной скоростью?

Эту задачу решает дифференциал, типичный «планетарный механизм». Механизм называется планетарным, если в нем есть вспомогательные механизмы, вращающиеся вокруг осей, которые, в свою очередь, вращаются.

Приводной вал через трансмиссию, дает вращение на первичную ось, а именно, через планетарный механизм, на первичный правый и левый валы-оси. С какой бы скоростью ни вращались задние колеса, скорость механизма всегда будет равна средней скорости карданных валов. Каждое колесо от дифференциала совершает много оборотов, пропорциональных длине его пути, так что в сумме вся энергия преобразуется в поступательное движение автомобиля.

Если автомобиль движется по прямой дороге, а под ведущими колесами находится грунт одинакового типа, т. е. с одинаковым коэффициентом трения, колеса принимают от механизма одинаковое количество оборотов, так что приводные валы вращаются (и колеса вместе с ними) с той же скоростью.

Но если коэффициенты трения разные, например, при прохождении одной стороной автомобиля над пятном масла или над слоем льда, то… как будут двигаться колеса, если это произойдет? Для неведущих колес это достаточно просто, так как они независимы друг от друга и не толкают машину, поэтому если одно из них оказывается на льду, оно перестает крутиться, и управляемость становится очень низкой.

Но теперь и левое заднее ведущее колесо оказывается на льду. Для правого колеса на асфальте управляемость высокая, а для левого колеса на льду она практически отсутствует. Следовательно, левое колесо крутится легче и начинает принимать на свою сторону все вращение, которое механизм делит на два вала.