Радиус или диаметр диска: Радиус или диаметр колеса: как правильно
Содержание
Как диаметр дисков влияет на поведение автомобиля
Диаметр дисков — один из ключевых параметров характеристики колесных дисков. От его величины зависит не только внешний вид колес, но и многое в поведение автомобиля на дороге.
Диаметр колесных дисков измеряется в дюймах. На настоящий момент многие ошибочно называют этот параметр колес радиусом.
Кроме того, замена штатных дисков на оригинальные или неоригинальные диски зачастую приводит к увеличению диаметра. Это один из самых простых и доступных видов внешнего тюнинга автомобиля.
Однако, делая выбор в пользу дисков того или иного размера, необходимо иметь представление о том, каким же образом диаметр дисков влияет на поведение автомобиля?
Увеличение диаметра автомобиля влияет на точность показателей спидометра. Именно поэтому, например, при рекомендованных дисках 17 диаметра заводом-производителем их замена на подобные колеса большего радиуса будет давать погрешность в среднем в 5-10 км/ч на спидометре в ту или иную сторону.
Это может доставить владельцу автомобиля большое количество неприятных моментов, связанных со штрафами с камер, фиксирующих реальную скорость автомобиля. Кроме того, в критической ситуации на дороге погрешность в скорости также может повлиять на решение совершить тот или иной маневр.
Диски большего размера несомненно обладают большим весом, поэтому общий вес автомобиля, хотя и незначительно, увеличивается. Это может привести к изменения показателей разгона и торможения и повысить расход топлива.
Больший диаметр колеса также повышает износ деталей подвески и ходовой части автомобиля. Именно поэтому следить за состоянием автомобиля придется более тщательно, так как нагрузка на подвеску существенно возрастает.
При увеличении диаметра дисков профиль резины уменьшается, поэтому при попадании в яму удар проходит непосредственно через колесо и части подвески непосредственно к амортизаторам автомобиля. Это также может существенно повысить их износ.
Это также может существенно повысить их износ.
Чем больше диаметр диска, тем жестче ощущаются все неровности дорожного покрытия. Из-за повышения нагрузки на все элементы подвески, большего пятна контакта с дорожным полотном и меньшей высоты профиля покрышки увеличивается жесткость при передвижении по прямой, прохождении поворотов и совершении маневров.
Увеличение диаметра диска также существенным образом влияет непосредственно на рулевое управление автомобилем. Увеличение пятна контакта с дорожным покрытием позволяет автомобилю более быстро и точно реагировать на каждое движение рулем, поэтому привычные маневры и стиль управления могут стать более резкими и более быстрыми.
Необходимо помнить, что каждое внесение изменений в штатную конструкцию автомобиля может существенным образом оказать влияние на безопасность при передвижении. Именно поэтому если вы задумались об увеличении радиуса дисков, необходимо придерживаться штатных параметров, рекомендованных для таких случаев конкретным заводом-производителем и за подбором колес обращаться только к квалифицированным специалистам.
AEZ Cliff есть на складе
Диаметры: R17, R18, R19, R20, R21
Цвет: HS, BFP
Цены: от 9 765 до 19 001 р.
Bremmer Kraft BR05 есть на складе
Диаметры: R20
Цвет: Bright PVD
Цены: уточняйте по тел.
Другие публикации
Установка датчика давления HUF
Двухминутное видео где рассказывается как устанавливать датчики давления HUF на любые диски
Читать полностью
Шипы и шины
Насколько разумно использование ошипованной резины, если она является причиной износа дорожного полотна и обладает повышенной шумливостью? С другой стороны использование обычной резины при укатаном снеге или гололеде увеличивает риск аварийности и вопрос безопасности в данном случае становится более важным. В конце концов, ремонт дорожного покрытия лежит на совести дорожных служб, а в нашей стране, как мы знаем дороги очень плохие, даже там где ошипованная резина не используется
Читать полностью
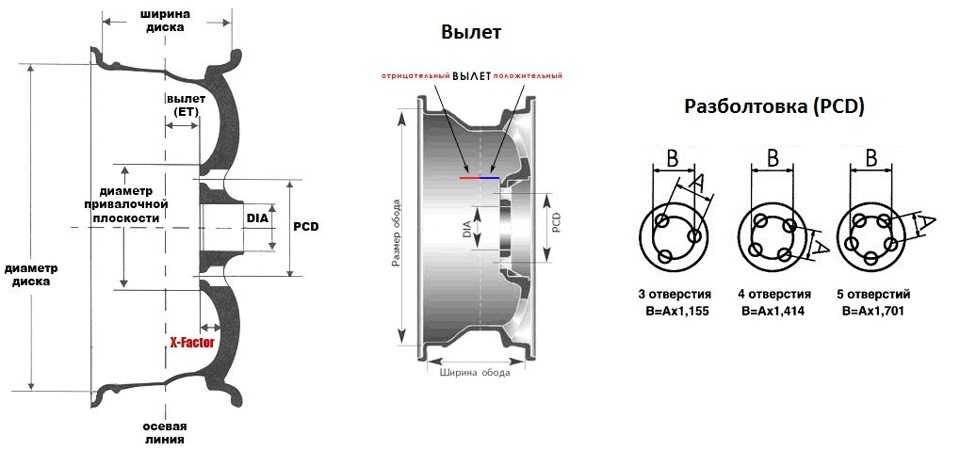
Что такое вылет?
Читать полностью
Уход за шинами
Для безопасности движение, а также для того, чтобы вы были спокойны за свою жизнь на дороге, необходимо правильно обращаться с шинами. Ниже мы приведем пять основных правил, которые необходимо выполнять для своего спокойствия.
Ниже мы приведем пять основных правил, которые необходимо выполнять для своего спокойствия.
Читать полностью
Как диски влияют на разгон и расход топлива
На каждом форуме, посвященном автомобильной тематике, можно найти темы, связанные с экономией топлива. Этот вопрос всегда будет в ТОПе. Несмотря на все рекламные кампании, водителям приходится искать альтернативные пути решения этой задачи. Возможно, если Вы садитесь за руль раз в неделю, то эта тема Вас не волнует. Но для водителей, которые постоянно за рулем, будет интересно узнать, как можно сэкономить. Сегодня чаще интересуются, как диски влияют на разгон и расход топлива? Скептики могут сказать, что никак, но практики постараются доказать обратное.
Влияние веса дисков
Неоднократно в сети встречались статьи, что тяжелый автомобиль будет расходовать больше топлива, чем аналогичная модель, но с меньшим весом. Водители стараются убрать с автомобиля все лишнее. Некоторые регулярно проводят чистку, чтобы в салоне или багажнике не оставалось ненужных вещей. Практичные задумываются над сменой стальных дисков на литые. Легкосплавные модели значительно легче стали, а значит, и вес автомобиля снижается. Как следствие, потребуется меньше топлива для прохождения конкретной дистанции.
Практичные задумываются над сменой стальных дисков на литые. Легкосплавные модели значительно легче стали, а значит, и вес автомобиля снижается. Как следствие, потребуется меньше топлива для прохождения конкретной дистанции.
Специалистами был проведен анализ, для которого взяли два авто с разным весом. Результат: каждые 500 кг увеличивают потребление топлива приблизительно на 700 л в год.
Увеличивая размер диска, Вы автоматически увеличиваете размеры покрышек, а значит, вес авто возрастает, что приводит к большему расходу топлива. Лучше устанавливать рекомендуемые производителем диски и шины.
Ширина дисков и покрышек
Гонясь за модными тенденциями, водители пренебрегают советами производителей, устанавливая широкие диски и шины. В качестве маленького эксперимента можно самостоятельно замерить расход. Первое, что будет тормозить – сопротивление воздуху. То есть автомобилю нужно будет больше «энергии», чтобы проехать определенное расстояние. Проведенные наблюдения подтвердили, что автомобили одной марки с разными дисками и покрышками расходуют различное количество литров топлива.
Если установить широкие колеса (в допустимых пределах от заводской комплектации), то разница составит около 0,5 л на 100 км. Для тех водителей, которые всегда за рулем, такая разница может стать ощутимой.
Диаметр диска и разгон авто
Было бы неправильно говорить только о разгоне автомобиля, обязательно нужно обращать внимание и на скорость торможения. В целом можно сделать обобщающий вывод, что на динамику авто влияет диаметр выбранных дисков. Как уже было сказано, увеличиваем диаметр – «растет» масса – снижается управляемость. Учтите, что, меняя колеса даже на 1 размер, можно получить внушительную разницу при разгоне. Шины (резина) по своей плотности будут легче металла, влияет только вес диска? Нет. Дело в том, что многие забывают об инерции, которая будет расти быстрее массы (имеется в виду процентное соотношение меньшего и большего размера). Наибольший вес дискам дает обод. Если взять две одинаковые покрышки и диски меньшего и большего диаметра, то момент инерции меньше будет у колес с меньшим диаметром дисков. Почему так важно учитывать инерцию? Инерция авто считается основной силой, которую преодолевает авто в процессе ускорения. Следующий раз, когда нужно будет преодолеть этот процесс – торможение. В автомобиле колеса являются единственной составляющей, которая начинает активно «работать» при нажатии педали газа, то есть, к ним подается энергия для вращения. И если колеса будут слишком тяжелыми, то потребуется значительно больше энергии и времени для того чтобы ускорить вращение и двинуться с места.
Почему так важно учитывать инерцию? Инерция авто считается основной силой, которую преодолевает авто в процессе ускорения. Следующий раз, когда нужно будет преодолеть этот процесс – торможение. В автомобиле колеса являются единственной составляющей, которая начинает активно «работать» при нажатии педали газа, то есть, к ним подается энергия для вращения. И если колеса будут слишком тяжелыми, то потребуется значительно больше энергии и времени для того чтобы ускорить вращение и двинуться с места.
Вывод
Можно выбрать диски меньшего диаметра и подобрать к ним более высокую резину, сохранив внешний диаметр по шине. Автомобиль будет лучше ехать. Почему? У меньшего диаметра диска меньше плечо приложения сил. Считается, что при отличном сцеплении с асфальтированным покрытием и небольшом диаметре колес будет быстрее разгон. Но, к сожалению, не всегда идеальное покрытие, и стопроцентное сцепление невозможно априори. Вся излишне подаваемая мощь уходит в буксировку, разгон на самом деле ограничивается сцеплением. Но и это можно исправить. Динамика улучшить, но только необходимо учитывать причины, а потом уже прибегать к конкретным действиям:
Но и это можно исправить. Динамика улучшить, но только необходимо учитывать причины, а потом уже прибегать к конкретным действиям:
- проблема в мощности авто — установите немного меньше диски, и сделать передачи более короткими;
- проблема в сцеплении с дорожным покрытием – можно попробовать широкую резину и диски чуть большего размера (в допустимых производителем диапазонах), сделав «длиннее» передачу.
В целом, старайтесь покупать диски, чтобы общий диаметр колес был как можно меньше. Ищите оптимальную середину по качеству, диаметру, весу и дизайну – избегайте крайности.
Выжать максималку можно с большими колесами, быстрее разогнаться и сэкономить на топливе позволят легкие колеса. Если снизить вес каждого колеса на килограмм, то это будет эквивалентно снижению веса в самом салоне авто на 40 кг. Ваш автомобиль поедет плавно и не потеряет своих разгонных характеристик.
Никогда не забывайте о качестве. От фирмы производителя многое зависит.
Как видно из всего выше описанного, выбор дисков имеет весомое значение для разгона, а вернее, для динамики авто. На длительных дистанциях легкие диски позволят почувствовать экономию на топливе. При этом категорически нельзя выбирать крайности: одинаково плохо слишком большой диаметр колес, и слишком маленький. Безусловно, много зависит от марки авто и производителя дисков и шин, доверяйте проверенным брендам, и тогда не придется платить лишнего.
Окружность, диск, сегмент, сектор. Формулы, характеристики и свойства круга
- Круг — определение
- Диск — определение
- Радиус и диаметр окружности
- Свойства круга
- Площадь и длина окружности
- Уравнение окружности
- Касательная окружности и ее свойства
- Секущая окружности и ее свойства
- Хорда окружности и ее свойства
- Центральный угол и вписанный угол окружности и его свойства
- Дуга окружности, длина дуги, стягивающий угол дуги
- Полукруг и полудиск
- Сектор, площадь сектора
- Сегмент, площадь сегмента
- Концентрическая окружность
- Кольцо
Определение.
Определение. Единичная окружность — это окружность, радиус которой равен единице.
Определение. Диск является частью плоскости, ограниченной окружностью.
Определение. Радиус окружности R – это расстояние от центра окружности О до любой точки окружности.
Определение. Диаметр окружности D — это отрезок, соединяющий две точки окружности и проходящий через ее центр.
Свойства окружности
1. Диаметр окружности равен двум радиусам.
D = 2r
2. Кратчайшее расстояние от центра окружности до секущей (хорды) всегда меньше радиуса.
3. Три точки, не лежащие на одной прямой, могут содержать только одну окружность.
4. Среди всех замкнутых кривых одинаковой длины наибольшую площадь имеет окружность.
5. Если две окружности соприкасаются в одной точке, то эта точка помещается на прямую, проходящую через центры окружностей.
Площадь и длина окружности
Длина окружности
1. Формула длины окружности через диаметр:
C = πD
2. Формула длины окружности через радиус:
C = 2πr
Формула площади круга
1. Формула площади круга через радиус:
A = πr 2
2. Формула площади круга через диаметр:
А = πD 2 4
Уравнение окружности
1. Уравнение окружности с радиусом r и центром в начале декартовой координаты:
r 2 = x 2 + y 2
2. Уравнение окружности радиусом r с центром в точке с координатами (a, b) в декартовой системе координат:
r 2 = (x — a) 2 + (y — b) 2
3.
| { | x = a + r cos t |
| y = b + r sin t |
Касательная окружности и ее свойства
Определение. Касательная — компланарная прямая, касающаяся окружности в одной точке.
Свойства касательной
1. Касательная всегда перпендикулярна радиусу окружности, проведенной в точке касания.
2. Кратчайшее расстояние от центра окружности до касательной – это радиус окружности.
3. Если две касательные из точек касания В и С одной и той же окружности не параллельны, то они пересекаются в точке А, а точка касания отрезка и точка пересечения касания есть тот же отрезок на другой касательной:
АВ = АС
Также, если провести линию через центр О и точку пересечения А этих касательных, то углы между этой линией и касательными будут равны:
∠ОАС = ∠ОАБ
Секущая окружности и ее свойства
Определение.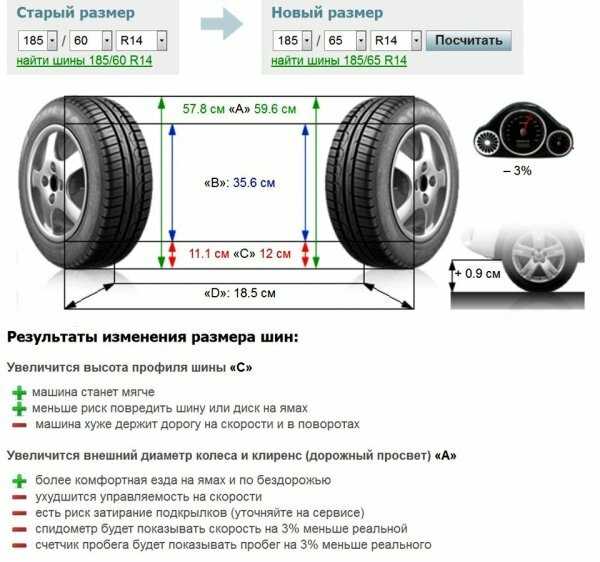 Секущая окружности — прямая, соединяющая две точки окружности.
Секущая окружности — прямая, соединяющая две точки окружности.
Свойства секущей окружности
1. Если точка вне круга (Q) получена двумя секущими, пересекающими окружность в двух точках А и В для первой секущей и С и D для другой секущей, то произведения двух пересекающихся отрезков равны:
AQ ∙ BQ = CQ ∙ DQ
2. Если точка Q выходит из секущей окружности, пересекающей окружность в двух точках А и В, и касания в точке касания С, то произведение секущих на отрезки равно квадрату касательной:
AQ ∙ BQ = CQ 2
Хорда окружности и ее свойства
Определение. Хорда окружности — это отрезок, соединяющий две точки окружности. Хорда — это отрезок касательной.
Длина хорды
1. Формула длины хорды через радиус и центральный угол:
АВ = 2r sin α2
2. Формула длины хорды через радиус и вписанный угол:
Формула длины хорды через радиус и вписанный угол:
АВ = 2r sin α
Свойства хорды
1. Две равные хорды, стягивающие две одинаковые дуги:
если хорды AB = CD, то
дуга ◡ AB = ◡ CD
2. Если хорды параллельны, дуги между ними будут одинаковыми:
если хорды AB ∣∣ CD, то
◡ AD = ◡ BC
3. Если радиус окружности перпендикулярен хорде, то он делит хорду пополам в точке пересечения:
если OD ┴ AB, то
AC = BC
4. Если две хорды AB и DE пересекаются в точке Q, то произведение отрезков, образованных при пересечении одной хорды, есть произведение отрезков хорды разных:
AQ ∙ BQ = DQ ∙ QC
5. Хорды равной длины равноудалены от центра окружности.
если хорды AB = CD, то
ON = OK
6.
если CD > AB, то
ON < OK
Центральный угол и вписанный угол окружности и его свойства
Определение. Центральный угол окружности угол, вершина которого является центром окружности.
Определение. Вписанный угол — это угол внутри окружности, вершина которого лежит на окружности.
Угловые свойства
1. Все вписанные углы, опирающиеся на одну дугу, равны (один конец хорды).
2. Вписанный угол будет прямым (90°), если он основан на диаметре окружности.
3. Любой вписанный угол всегда равен половине центрального угла, опирающегося на ту же дугу
β = α2
4. Если два вписанных угла опираются на хорду и расположены по обе стороны от нее, то сумма углов равна 180°.
α + β = 180°
Определение. Дуга окружности (◡) является частью окружности, соединяющей две точки на окружности.
Дуга окружности (◡) является частью окружности, соединяющей две точки на окружности.
Определение. Стягивающий угол дуги — это угол между двумя радиусами, ограничивающими эту дугу. Стягивающий угол дуги всегда равен центральному углу между радиусами, ограничивающими конечные точки этой дуги.
Формула длины дуги через центральные углы (в градусах) и радиус:
л = πr180°∙ α
Определение. Полуокружность – дуга, концы которой соединены диаметром окружности.
Определение.
Определение. Сектор (◔) является частью диска, который ограничен двумя радиусами и дугой между радиусами.
Формула. Формула площади сектора через радиус и центральные углы (в градусах)
А = πr 2 360°∙ α
Определение. Отрезок является частью диска, который ограничен дугой и хордой, соединяющей концы этой дуги.
Определение. Концентрическая окружность — это окружность с разными радиусами, имеющая общий центр.
Определение. Кольцо является частью плоскости, ограниченной двумя концентрическими окружностями.
Формулы геометрии Квадрат. Формулы и свойства квадрата Прямоугольник. Формулы и свойства прямоугольника Параллелограмм. Формулы и свойства параллелограмма Ромб. Формулы и свойства ромба Круг, диск, сегмент, сектор. Формулы и свойства Эллипс. Формулы и свойства эллипса Цилиндр. Формулы и свойства цилиндра Конус. Формулы, характеристики и свойства конуса Площадь. Формулы площади Периметр. Формулы периметра Объем. Формулы объема Формулы площади поверхности
Все таблицы и формулы
Диск Млечного Пути больше, чем мы думали
Предоставлено: Instituto de Astrofisica de Canarias (IAC). Группа исследователей из Института астрофизики Канарских островов (IAC) и Национальной астрономической обсерватории Пекина (NAOC) опубликовала статью, в которой предполагается, что если бы мы могли путешествовать со скоростью света, нам потребовалось бы 200 000 лет, чтобы пересечь диск нашей галактики.
Спиральные галактики, такие как Млечный Путь, имеют очень тонкие диски, в которых находится большая часть их звезд. Эти диски имеют ограниченный размер, так что за пределами определенного радиуса остается очень мало звезд.
В нашей галактике мы не знали, что в диске есть звезды на расстояниях от центра, более чем в два раза превышающих расстояние от Солнца. Это означает, что наша собственная звезда, по-видимому, вращалась примерно на половине галактического радиуса. Однако теперь мы знаем, что есть звезды намного дальше, более чем в три раза превышающие это расстояние, и вполне вероятно, что некоторые звезды находятся более чем в четыре раза дальше Солнца от галактического центра.
«Диск нашей галактики огромен, около 200 тысяч световых лет в диаметре», — говорит Мартин Лопес-Корредоира, исследователь IAC и первый автор статьи, недавно опубликованной в журнале Astronomy & Astrophysics . и чьи авторы происходят как из IAC, так и из NAOC.
В общих чертах, мы можем думать о галактиках, подобных Млечному Пути, как о состоящих из вращающегося диска со спиральными рукавами и гало сферической формы, которое его окружает. В этой части исследования сравнивалось содержание металлов (тяжелых элементов) в звездах галактической плоскости с содержанием гало, чтобы обнаружить, что существует смесь звезд диска и гало на указанных больших расстояниях.
В этой части исследования сравнивалось содержание металлов (тяжелых элементов) в звездах галактической плоскости с содержанием гало, чтобы обнаружить, что существует смесь звезд диска и гало на указанных больших расстояниях.
Исследователи пришли к таким выводам после статистического анализа данных исследований APOGEE и LAMOST, двух проектов, которые получают спектры звезд для извлечения информации об их скоростях и химическом составе. «Используя металличности звезд в каталогах из высококачественных спектральных атласов APOGEE и LAMOST, а также расстояния, на которых расположены объекты, мы показали, что существует заметная доля звезд с более высокой металличностью, характерной для диска звезды, дальше, чем ранее предполагаемый предел радиуса галактического диска», — объясняет Карлос Альенде, исследователь IAC и соавтор этой публикации.
Франсиско Гарсон, исследователь IAC, который является еще одним из авторов статьи, объясняет: «Мы не использовали модели, которые иногда дают нам только ответы, для которых они были разработаны, но мы использовали только статистику большого числа объектов.
