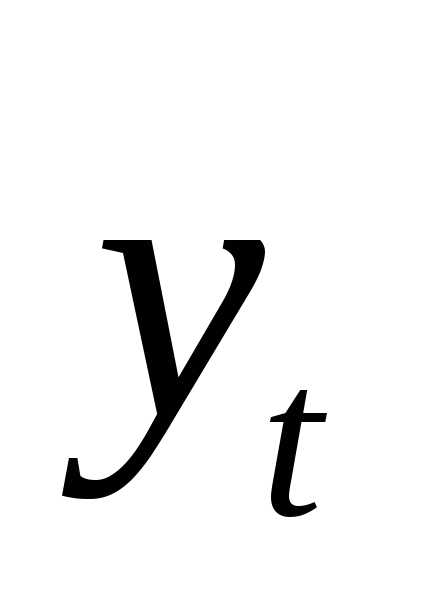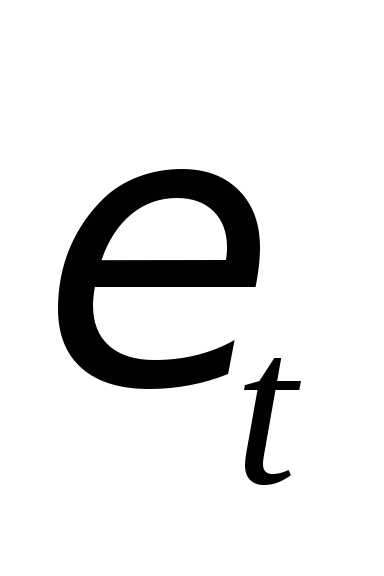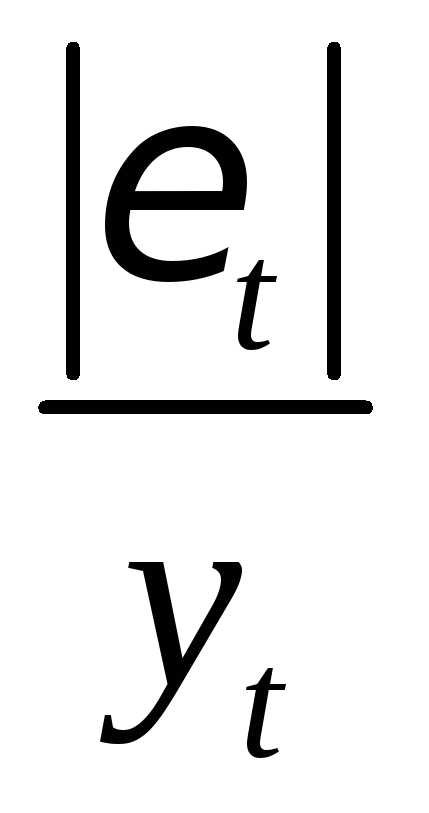Оценка параметров модели по формуле (3.5) «вручную». Модель формула 40
Модельформ 40+ – инструкция по применению, отзывы, цена, аналоги
Общеизвестный препарат «Виагра» изначально разрабатывался для лечения артериальной гипертонии.
В четырех дольках темного шоколада содержится порядка двухсот калорий. Так что если не хотите поправиться, лучше не есть больше двух долек в сутки.
Самое редкое заболевание – болезнь Куру. Болеют ей только представители племени фор в Новой Гвинее. Больной умирает от смеха. Считается, что причиной возникновения болезни является поедание человеческого мозга.
Человеческие кости крепче бетона в четыре раза.
В течение жизни среднестатистический человек вырабатывает ни много ни мало два больших бассейна слюны.
Американские ученые провели опыты на мышах и пришли к выводу, что арбузный сок предотвращает развитие атеросклероза сосудов. Одна группа мышей пила обычную воду, а вторая – арбузный сок. В результате сосуды второй группы были свободны от холестериновых бляшек.
Если улыбаться всего два раза в день – можно понизить кровяное давление и снизить риск возникновения инфарктов и инсультов.
При регулярном посещении солярия шанс заболеть раком кожи увеличивается на 60%.
Работа, которая человеку не по душе, гораздо вреднее для его психики, чем отсутствие работы вообще.
Желудок человека неплохо справляется с посторонними предметами и без врачебного вмешательства. Известно, что желудочный сок способен растворять даже монеты.
Существуют очень любопытные медицинские синдромы, например, навязчивое заглатывание предметов. В желудке одной пациентки, страдающей от этой мании, было обнаружено 2500 инородных предметов.
Наши почки способны очистить за одну минуту три литра крови.
В Великобритании есть закон, согласно которому хирург может отказаться делать пациенту операцию, если он курит или имеет избыточный вес. Человек должен отказаться от вредных привычек, и тогда, возможно, ему не потребуется оперативное вмешательство.
Ученые из Оксфордского университета провели ряд исследований, в ходе которых пришли к выводу, что вегетарианство может быть вредно для человеческого мозга, так как приводит к снижению его массы. Поэтому ученые рекомендуют не исключать полностью из своего рациона рыбу и мясо.
На лекарства от аллергии только в США тратится более 500 млн долларов в год. Вы все еще верите в то, что способ окончательно победить аллергию будет найден?
Модельформ для возраста 40+ | Модельформ
Инструкция по применению
Биологически активная добавка к пище МОДЕЛЬФОРМ 40+ (MODELFORM 40+) на основе растительных экстрактов. Для лиц, контролирующих массу тела.
Специально для женщин после 40 лет немецкая компания FARMAPLANT® Fabrikation Chemischer Produkte GmbH (Germany) предлагает инновационное средство MODELFORM 40+.
Форма выпуска и упаковка:
Капсулы массой 380 мг, расфасованные по 15 шт. в блистере (в упаковке 2 блистера).
Общая информация:
Биологически активная добавка к пище MODELFORM 40+ содержит инновационный комплекс ELEGREENALL, который дополнительно усилен натуральными ингредиентами.
Применение MODELFORM 40+ способствует:
- снижению массы тела;
- регулированию аппетита;
- улучшению функционального состояния желудочно-кишечного тракта;
- улучшению общего самочувствия;
- снижению жировой массы тела (жировых отложений).
- оказывает общеукрепляющее действие на женщин в период пре- и постменопаузы.
MODELFORM 40+ содержит компоненты, обладающие мягким тонизирующим эффектом и способствующие регулированию усвоения жиров и углеводов, поступающих в организм с пищей, очищению организма от токсинов, попадающих извне и образующихся в процессе обмена веществ.
Состав:
Innovative complex ELEGREENALL (Инновационный комплекс ЭЛЕГРИНОЛ) (экстракт померанца горького 10 %, экстракт мушмулы японской, псиллиум), форсколин 10 %, экстракт момордики харанции, порошковый экстракт пуэрарии.
Инновационный комплекс ELEGREENALL включает:
- экстракт померанца горького — источник синефрина, который активизирует метаболизм, может подавлять аппетит, способствуя снижению массы тела. Стимулирует в организме термогенез, ускоряет процесс расщепления жиров — активирует жировой обмен. Обладает мягким тонизирующим действием: повышает активность, снимает усталость 123.
- псиллиум — пищевые волокна, которые облегчают снижение массы тела. Они обеспечивают более длительное чувство насыщения, что позволяет сократить объем потребляемой пищи, способствуют сбалансированному усвоению жиров и углеводов, нормализации пищеварения, регулируют работу кишечника.
- экстракт мушмулы японской содержит в большом количестве коросолиевую кислоту, калий, витамин С и провитамин А. В ходе проведенных экспериментов доказано влияние на улучшение обмена веществ, снижение уровня липидов, сахара в крови, что способствует снижению жировой массы тела 56.
Именно для женщин после 40 лет инновационный комплекс ELEGREENALL дополнительно усилен ингредиентами:
- форсколин — натуральное вещество, получаемое из растения Coleus forskohlii (Колеус форсколии). Исследования показали, что экстракт колеуса форсколии активизирует процесс обмена веществ, уменьшает аппетит, способствует снижению жировой массы тела 789.
- экстракт момордики харанции — содержит большое количество кальция, калия, магния и железа. Регулирует аппетит, улучшает пищеварение, способствует более эффективному расщеплению жиров. Водорастворимые компоненты момордики оказывают влияние на ферменты детоксикации, которые выводят из организма токсины, попадающие извне и образующиеся в процессе обмена веществ 10. В ходе эксперимента выявлена способность к снижению уровня сахара в крови. 11.
- порошковый экстракт пуэрарии — содержит фитоэстрогены (генистеин и даидзеин)12, способствующие поддержанию уровня гормонального баланса, нарушение которого влечет за собой набор лишнего веса у женщин в период пре- и постменопаузы. Экстракт пуэрарии восстанавливает силы, обладает общеукрепляющим действием, оказывает положительное влияние на репродуктивные органы, сердечно-сосудистую систему и липидный обмен 1314.
Рекомендации по применению:
Взрослым по 1 капсуле в первой половине дня во время еды или после приема пищи, запивая достаточным количеством воды (200 мл). Продолжительность приема — 2 месяца. При необходимости прием можно повторить.
Продолжительность приема
2 месяца. При необходимости курс можно повторить.
Область применения:
через аптечную сеть и специализированные магазины, отделы торговой сети в качестве биологически активной добавки к пище, источника синефрина, содержит коросолиевую кислоту, форсколин.
Дата изготовления:
см. на упаковке
Условия хранения
хранить в сухом, защищенном от прямых солнечных лучей и недоступном для детей месте, при температуре не выше 25 ˚С.
Противопоказания
индивидуальная непереносимость компонентов БАД, беременность, кормление грудью.
Срок годности
3 года
Перед применением рекомендуется проконсультироваться с врачом. Не является лекарством.
Более подробную информацию узнайте на сайте www.modelform.ru Телефон горячей линии: 8 (800) 555-17-97 СГР № RU.77.99.11.003.Е.009556.10.14 от 20.10.2014 г.
линия натуральных средств для снижения веса
Мы провели обширные исследования: изучили опыт применения, содержание и эффективность всех существующих методик в области снижения веса.Мы рады поделиться с вами результатами нашей работы. Представляем вашему вниманию MODELFORM.
MODELFORM линия натуральных средств для снижения веса и моделирования форм, которая создана высококлассными специалистами на основе самых прогрессивных разработок.
Все средства для снижения веса MODELFORM имеют удобный режим приема: всего 1 капсула в день!
Мы первые, кто применил в практике снижения веса избирательный подход «18/30/40», который учитывает возрастные особенности женского организма.
Каждое средство для снижения веса MODELFORM содержит инновационный комплекс ELEGREENALL, который усилен натуральными ингредиентами. Они подобраны в соответствии с нюансам в причинах набора веса у женщин разного возраста.
Помимо основных причин набора веса в молодом возрасте, свой существенный вклад в появление лишнего веса и формирование жировых отложений вносят злоупотребление «нездоровой» пищей (фаст-фуд, мучное, сладкое, газированные напитки) и несоблюдение режима питания.
Специально для молодых женщин от 18 лет разработано инновационное средство для снижения веса MODELFORM 18+ , которое влияет не только на классический набор причин лишнего веса, но и способствует уменьшению тяги к мучному и сладкому.
С возрастом в организме женщины замедляется обмен веществ, вследствие чего накапливаются «шлаки» и токсины, это становится еще одной причиной набора лишнего веса и усложняет борьбу за стройность. Специально для женщин после 30 лет было разработано инновационное средство для снижения веса MODELFORM 30+ , которое влияет не только на классический набор причин лишнего веса, но и способствует очищению организма от токсинов, поступающих извне и образующихся в процессе обмена веществ.
Женщины после сорока лет, даже несмотря на внимательное отношение к своему рациону и регулярные занятия спортом, начинают прибавлять в весе. Причина кроется в снижении уровня гормонов, что в свою очередь ведет к еще большему замедлению обменных процессов, набору лишних килограммов, а также постепенному увеличению жировых отложений в области бедер и талии.
Специально для женщин после 40 лет разработано инновационное средство для снижения веса MODELFORM 40+, которое влияет не только на классический набор причин лишнего веса, но и способствует поддержанию уровня гормонального баланса, оказывает общеукрепляющее действие на женщин в период пре- и постменопаузы.
Компания Farmaplant ® Fabrikation Chemischer Produkte GmbH (Germany) предлагает инновационное средство для снижения веса женщин после родов и окончания периода грудного вскармливания – «МОДЕЛЬФОРМ (MODELFORM) СТРОЙНАЯ МАМА». Рецептура «МОДЕЛЬФОРМ (MODELFORM) СТРОЙНАЯ МАМА» специально разработана с учётом особенностей физиологических процессов, проходящих в организме женщины в течение 18 месяцев после родов.*
Благодаря входящим в состав компонентам, «МОДЕЛЬФОРМ (MODELFORM) СТРОЙНАЯ МАМА» способствует восстановлению и защите организма женщины после родов и окончания периода грудного вскармливания, а также приведению фигуры и массы тела к максимально приближенному состоянию «до беременности».
В соответствии с философией MODELFORM «18/30/40» наши эксперты подготовили авторскую систему питания и комплекс упражнений, которые также адаптированы к разным возрастным периодам.
Средства MODELFORM, желание меняться, вера в победу и готовность соблюдать все наши рекомендации помогут вам обрести стройное и привлекательное тело!
Снижать вес и моделировать свои формы теперь возможно в любом возрасте!

Formula 40 Pc в б/у судах
Чтобы начать поиск судна, активируйте Javascript в Вашем браузере
Formula 40 Pc в разделе подержанных и б/у судов на TopBoats.com. Сравните цены и найдите лучшие предложения по продаже Formula. Модель 40 Pc и другие модели марки Formula по лучшей цене в продаже от профессионалов и частных лиц.
TopBoatsСписок подержанных судов модели 40 Pc. Это одна из основных моделей Formula, которые вы можете найти на TopBoats.com в продаже от профессионалов и частных лиц. Если Вы подумываете о покупке Formula, рассмотрите эту модель 40 Pc. Вы можете найти больше информации, например, комментарии или среднюю цену в зависимости от года выпуска в разных разделах этой страницы.
Отправьте мне уведомления по параметрам этого поиска: Б/у суда Formula в Весь мир
Введите свой адрес электронной почты
США
Beaufort (South Carolina), СШАЦЕНЫ СОКРАТИЛИСЬ, ЧТО ПРЕДЛАГАЮТ, ЧТО ТАКОЕ НИЗКИЙ ЦЕННЫЙ ДИЗЕЛЬНЫЙ 40-дюймовый ПК «FORMULA» В МИРЕ ЭТО ЦЕНА НИЖНЕЙШЕ, ЧЕМ СРАВНЕНИЕ ГАЗОВ И ...
США
Suffolk (New York), США- Фондовый # 061470 - Если вы находитесь на рынке крейсера, посмотрите не дальше, чем в 2001 году на ПК «Формула-40», только что сократившись ...
Результаты в других странах
США
Beaufort (South Carolina), СШАЦЕНЫ СОКРАТИЛИСЬ, ЧТО ПРЕДЛАГАЮТ, ЧТО ТАКОЕ НИЗКИЙ ЦЕННЫЙ ДИЗЕЛЬНЫЙ 40-дюймовый ПК «FORMULA» В МИРЕ ЭТО ЦЕНА НИЖНЕЙШЕ, ЧЕМ СРАВНЕНИЕ ГАЗОВ И ...
США
Suffolk (New York), США- Фондовый # 061470 - Если вы находитесь на рынке крейсера, посмотрите не дальше, чем в 2001 году на ПК «Формула-40», только что сократившись ...
Последние комментарии об этой модели Formula 40 pc
Средняя цена на Formula 40 pc
Основные модели Formula
Оценка параметров модели по формуле (3.5) «вручную».
Промежуточные расчеты параметров линейной модели по формулам (3.5)приведены в табл. 4.3.15.
Табл. 4.3.15
| № |
| | | |
|
| |
| 1 | 45 | -5,5 | 30,25 | -5 | 27,5 | 40,04 | 4,96 |
| 2 | 40 | -4,5 | 20,25 | -10 | 45 | 41,85 | -1,85 |
| 3 | 43 | -3,5 | 12,25 | -7 | 24,5 | 43,66 | -0,66 |
| 4 | 48 | -2,5 | 6,25 | -2 | 5 | 45,47 | 2,53 |
| 5 | 42 | -1,5 | 2,25 | -8 | 12 | 47,28 | -5,28 |
| 6 | 47 | -0,5 | 0,25 | -3 | 1,5 | 49,09 | -2,09 |
| 7 | 51 | 0,5 | 0,25 | 1 | 0,5 | 50,91 | 0,09 |
| 8 | 55 | 1,5 | 2,25 | 5 | 7,5 | 52,72 | 2,28 |
| 9 | 50 | 2,5 | 6,25 | 0 | 0 | 54,53 | -4,53 |
| 10 | 57 | 3,5 | 12,25 | 7 | 24,5 | 56,34 | 0,66 |
| 11 | 60 | 4,5 | 20,25 | 10 | 45 | 58,15 | 1,85 |
| 12 | 62 | 5,5 | 30,25 | 12 | 66 | 59,96 | 2,04 |
| 6,5 | 50 | 143 | 259 | 0 |
При вычислении «вручную» по формуле (3.4)получаем те же результаты:
,
Табл. 4.3.16.
| A | B | C | D | E | F | G | H | |
| 1 | ВЫЧИСЛЕНИЯ В EXCEL С ИСПОЛЬЗОВАНИЕМ ФОРМУЛ | |||||||
| 2 | № |
| | | |
|
|
|
| 3 | 1 | 45 | =B2-$J$15 | =D2*D2 | =C2-$K$15 | =D2*F2 | =$M$21+$M$18*B2 | =C2-h3 |
| 4 | 2 | 40 | =B3-$J$15 | =D3*D3 | =C3-$K$15 | =D3*F3 | =$M$21+$M$18*B3 | =C3-h4 |
| 5 | 3 | 43 | =B4-$J$15 | =D4*D4 | =C4-$K$15 | =D4*F4 | =$M$21+$M$18*B4 | =C4-h5 |
| 6 | 4 | 48 | =B5-$J$15 | =D5*D5 | =C5-$K$15 | =D5*F5 | =$M$21+$M$18*B5 | =C5-H5 |
| 7 | 5 | 42 | =B6-$J$15 | =D6*D6 | =C6-$K$15 | =D6*F6 | =$M$21+$M$18*B6 | =C6-H6 |
| 8 | 6 | 47 | =B7-$J$15 | =D7*D7 | =C7-$K$15 | =D7*F7 | =$M$21+$M$18*B7 | =C7-H7 |
| 9 | 7 | 51 | =B8-$J$15 | =D8*D8 | =C8-$K$15 | =D8*F8 | =$M$21+$M$18*B8 | =C8-H8 |
| 10 | 8 | 55 | =B9-$J$15 | =D9*D9 | =C9-$K$15 | =D9*F9 | =$M$21+$M$18*B9 | =C9-H9 |
| 11 | 9 | 50 | =B10-$J$15 | =D10*D10 | =C10-$K$15 | =D10*F10 | =$M$21+$M$18*B10 | =C10-h20 |
| 12 | 10 | 57 | =B11-$J$15 | =D11*D11 | =C11-$K$15 | =D11*F11 | =$M$21+$M$18*B11 | =C11-h21 |
| 13 | 11 | 60 | =B12-$J$15 | =D12*D12 | =C12-$K$15 | =D12*F12 | =$M$21+$M$18*B12 | =C12-h22 |
| 14 | 12 | 62 | =B13-$J$15 | =D13*D13 | =C13-$K$15 | =D13*F13 | =$M$21+$M$18*B13 | =C13-h23 |
| 15 | =СРЗНАЧ (A2:A13) | =СРЗНАЧ (B2:B13) |
| =СУММ (D2:D13) |
| =СУММ (F2:F13) |
| =СУММ (h3:h23) |
| a1= | =G14/E14 | |||||||
| a0= | =C14-E17*B14 | |||||||
оценка качества построенной модели.
2.1) Оценка адекватности
Для оценки адекватности построенных моделей исследуются свойства остаточной компоненты, т.е. расхождения уровней, рассчитанных по модели, и фактических наблюдений (табл. 4.3.17).
Табл. 4.3.17.
| № | | Точки поворота | | |
| 1 | 4,962 |
| 24,617 |
|
| 2 | -1,850 | * | 3,421 | 46,392 |
| 3 | -0,661 |
| 0,437 | 1,413 |
| 4 | 2,528 | * | 6,391 | 10,169 |
| 5 | -5,283 | * | 27,912 | 61,015 |
| 6 | -2,094 |
| 4,387 | 10,169 |
| 7 | 0,094 |
| 0,009 | 4,791 |
| 8 | 2,283 | * | 5,213 | 4,791 |
| 9 | -4,528 | * | 20,503 | 46,392 |
| 10 | 0,661 |
| 0,437 | 26,924 |
| 11 | 1,850 |
| 3,421 | 1,413 |
| 12 | 2,038 |
| 4,155 | 0,036 |
|
| 0 | 5 | 100,902 | 213,504 |
При проверке независимости(отсутствие автокорреляции) определяется отсутствие в ряду остатков систематической составляющей, например, с помощью d-критерия Дарбина–Уотсона по формуле(3.7):
Так как  попало в интервал отd2, до 2 то по данному критерию можно сделать вывод о выполнении свойства независимости.
попало в интервал отd2, до 2 то по данному критерию можно сделать вывод о выполнении свойства независимости.
Это означает, что в ряду динамики не имеется автокорреляции, следовательно, модель по этому критерию адекватна.
Неравенство выполняется (5>4). Следовательно, свойство случайности выполняется. Модель по этому критерию адекватна.
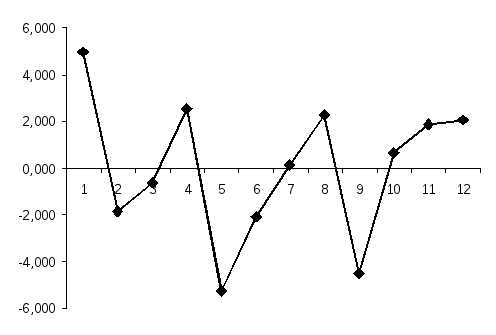
Рис. 3.4.14. График остатков
RS= max –
max – min/
min/  ;
;
где  max – максимальный уровень ряда остатков,
max – максимальный уровень ряда остатков,  max=4,962;
max=4,962;
 min – минимальный уровень ряда остатков,
min – минимальный уровень ряда остатков,  min=– 4,528;
min=– 4,528;
 – среднеквадратическое отклонение,
– среднеквадратическое отклонение,
 =
=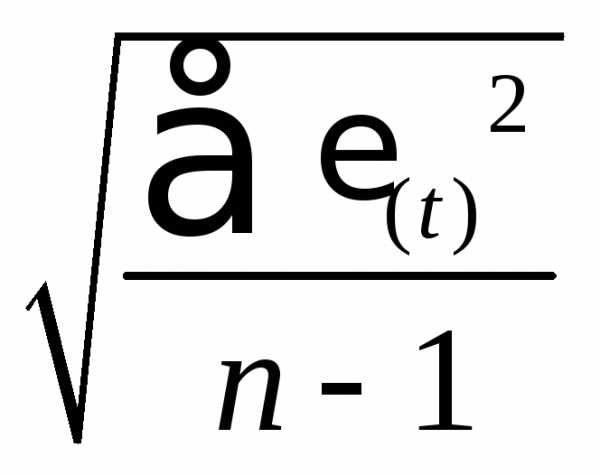 =
=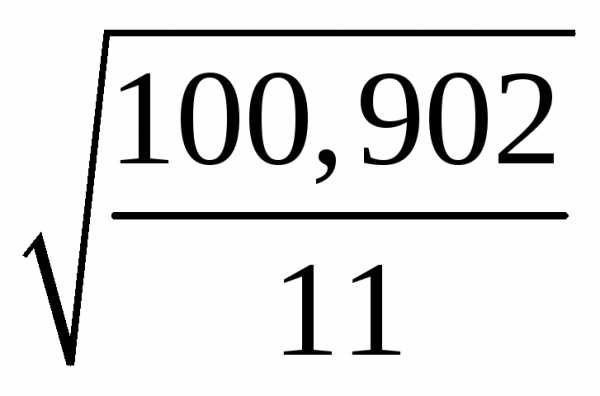 =3,029;
=3,029;
RS=4,962–(–5.283)/ 3,029= 3,383
Расчетное значение попадает в интервал (2,7 – 3,7), следовательно, выполняется свойство нормальности распределения. Модель по этому критерию адекватна.
В нашем случае  = 0, поэтому гипотеза о равенстве математического ожидания значений остаточного ряда нулю выполняется.
= 0, поэтому гипотеза о равенстве математического ожидания значений остаточного ряда нулю выполняется.
В табл. 4.3.18собраны данные анализа ряда остатков.
Таблица4.3.18.Анализ ряда остатков
| Проверяемое свойство | Используемые статистики | Граница | Вывод | |||
| наименование | значение | нижняя | верхняя | |||
| Независимость | d-критерий Дарбина–Уотсона r(1) – коэффициент автокорреляции | d=2,12 dn=4-2,21=1,88 | 0,98 | 1,36 0,36 | адекватна | |
| Случайность | Критерий пиков (поворотных точек) | 5 > 4 | 4 | адекватна | ||
| Нормальность | RS-критерий | 3,383 | 2,6 | 2,7 | адекватна | |
| Среднее | t-статистика Стьюдента | 0,000 | -2,179 | 2,179 | адекватна | |
| Вывод: Модель статистически адекватна | ||||||
2.2) Оценка точности
Для оценки точности модели вычислим среднюю относительную ошибку аппроксимации 
Таблица4.3.19.
| Номер наблюдения | | | |
| 1 | 45 | 4,96 | 0,110 |
| 2 | 40 | -1,85 | 0,046 |
| 3 | 43 | -0,66 | 0,015 |
| 4 | 48 | 2,53 | 0,053 |
| 5 | 42 | -5,28 | 0,126 |
| 6 | 47 | -2,09 | 0,045 |
| 7 | 51 | 0,09 | 0,002 |
| 8 | 55 | 2,28 | 0,042 |
| 9 | 50 | -4,53 | 0,091 |
| 10 | 57 | 0,66 | 0,012 |
| 11 | 60 | 1,85 | 0,031 |
| 12 | 62 | 2,04 | 0,033 |
- хороший уровень точности модели.
Модель Чессера и модель Змиевского. Пример расчета в Excel
Рассмотрим модель Чессера и модель Змиевского оценки вероятности банкротства у предприятия. С помощью них можно провести экспресс-диагностику финансового состояния предприятия или оценить кредитоспособность предприятия. Рассмотрим две модели одна, из которых была построена на инструментарии logit-регрессии, а другая на инструментарии probit-регрессии. Обе эти модели являются разновидностями моделей бинарного выбора, где в результате можно отнести предприятие либо к классу банкротов либо к классу небанкротов.
Что такое logit/probit-модель оценки финансового состояния предприятия?
Logit/probit-модели – статистические прогнозные модели, которые позволяют оценить вероятность наступления банкротства у предприятия. Как правило, прогноз составляет интервал от 1 до 3 лет. Для ее разработки используются две выборки предприятий: одна группа предприятий банкротов по решению арбитражного суда, а другая группа предприятий финансово устойчивых. Для этих групп предприятий рассчитываются финансовые коэффициенты, а затем с помощью инструментария логистической регрессии строится регрессионная модель наиболее точно описывающая эти две выборки.
Отличие logit-модели от probit-модели заключается в том, что первая дает значение от 0 до 1, а вторая только бинарное значение 0 или 1, где 0 в данном случае означает, что предприятие финансово устойчиво, а 1 – банкрот.
| Logit-модель | Probit-модель | |
| Модель используется | в медицине, социологии, в экономике | в социологии, медицине (токсикологии) |
| Разработка математического инструментария | 50-60-е года 20 века | 30-40-е года 20 века |
| Результат использования | Значение в интервале от 0 до 1 | Бинарное значение 0 или 1 |
| Используемое распределение | Логистическое | Нормальное |
Кем используются модели оценки финансового состояния?
Основные пользователи данных моделей являются банки, которые оценивают предприятия на предмет его кредитоспособности. Изначально именно банки оценивали с помощью них кредитоспособность заемщика. Помимо этого такие модели оценки можно использовать самим предприятиям в качестве собственной экспресс-диагностики финансового положения, а также для финансовой оценки своих партнеров. Перейдем к разбору первой модели оценки платежеспособности – модели Чессера.
Модель Чессера (1974 г.)
В 1974 году Д. Чессер разработал одну из первых logit-моделей оценки финансового состояния предприятия (Chesser, Delton «Predicting loan noncompliance», Journal of commercial bank lending, 1974). Модель была создана для банков с целью оценки кредитоспособности заемщиков. Для ее построения Чессер использовал данные банков по 37 неудовлетворительным займам и 37 удовлетворительным.
Формула расчета модели
Z= -2.0434 – 5.24*X1 + 0.0053*X2 – 6.6507*X3 + 4.4009*X4 – 0.0791*X5 – 0.102*X6
P = 1/(1+e—z)
| Коэффициент | Формула расчета | Расчет по РСБУ |
| Х1 | (Наличность + Легко реализуемые ценные бумаги) / Активы | (стр.1250+стр.1240) / стр.1600 |
| Х2 | Нетто-продаж / (Наличность + Легко реализуемые ценные бумаги) | стр.2110 / (стр.1250+стр.1240) |
| Х3 | (Брутто-доходы) / Активы | (стр.1200-стр.1500) / стр.1600 |
| Х4 | (Краткосрочная + Долгосрочная задолженность) / Активы | (стр. 1400+стр.1500) / стр.1600 |
| Х5 | Основной капитал / Чистые активы | стр.1300 / см. примечание |
| Х6 | Оборотный капитал / (Нетто-продажи) | (стр.1200 – стр.1500) / стр.2110 |
Примечание:
P – вероятность банкротства предприятия(значение показателя находится в интервале от 0 до 1)
В коэффициенте Х3 в числителе стоит «Нетто-продаж», которое равно Выручке от продаж.
В коэффициенте Х2 в знаменателе используются «Легко реализуемые ценные бумаги», которое условно можно приравнять к «Финансовым вложениям» по РСБУ. Повторю, что условно.
В коэффициенте Х5 используются «Чистые активы», чтобы их рассчитать можно воспользоваться Приказом Минфина России от 28.08.2014 №84н «Об утверждении Порядка определения стоимости чистых активов».
Оборотный капитал = чистый оборотный капитал = рабочий капитал.
Экспресс-оценка финансового состояния по модели Чессера
Если P<0.5, то можно сделать вывод, что финансовое положение у предприятия стабильное и риск банкротства невелик.
Детальная оценка финансового состояния по модели
В зависимости от различной оценки вероятности можно сделать более детальный вывод о финансовом состоянии предприятия. Ниже в таблице представлены интервалы оценки вероятности банкротства предприятия и его характеристика финансового состояния.
| Вероятность банкротства | Характеристика финансового состояния предприятия |
| 0.8<P<1 | Финансовое положение предприятия критическое |
| 0.6<P<0.8 | Платежеспособность предприятия на грани риска банкротства |
| 0.4<Р<0.6 | Финансовое состояние предприятия удовлетворительное |
| 0.2<Р<0.4 | Кредитоспособность предприятия на хорошем уровне |
| 0<Р<0.4 | Финансовое положение предприятия отличное |
Модель Змиевского (1984 г.)
В 1984 году М. Змиевский предлагает одну из первых probit-моделей оценки финансового состояния предприятия (Zmijewski, M., E., Methodological issues related to the estimation of financial distress prediction models, Journal of accounting research 24, 1984). Модель строилась на основании трех финансовых коэффициентов, а также на выборке 40 предприятий банкротов и 800 предприятий небанкротов с 1972 по 1978 года с NYSE. Для формирования модели использовался инструментарий probit-регрессии.
Формула расчета модели
Z = -4.3 — 4.5*X1 + 5.7*X2 – 0.004*X3
P = f(Z)
| Коэффициент | Формула расчета | Расчет по РСБУ | Расчет по МСФО |
| X1 | Чистая прибыль / Активы | стр.2400 / стр.1600 | Net income / Total assets |
| X2 | (Долгосрочные обязательства + Краткосрочные обязательства) / Активы | (стр.1400+стр.1500) / стр.1300 | Total debt / Total assets |
| X3 | Оборотные активы / Краткосрочные обязательства | стр. 1200 / стр. 1500 | Current assets / Current liabilities |
Примечание:
f – функция стандартного нормального распределения. Стандартное нормальное распределение имеет математическое ожидание 0 и стандартное отклонение 1.
Р – вероятность банкротства.
Расчет probit-модели Змиевского в Excel
Для примера рассмотрим расчет пробит-модели оценки финансового состояния предприятия в Excel.
Модель Змиевского оценки платежеспособности предприятия
Х1 – Х3 – финансовые коэффициенты в probit-модели Змиевского.
Z – интегральное значение по модели.
f(Z) — функция стандартного нормального распределения.
P — бинарная величина принимающая значение 0 или 1 (небанкрот / банкрот).
Чтобы определить существует ли риск банкротства у предприятия необходимо рассчитать функцию стандартного нормального распределения. В Excel для этого подходит две формулы:
=НОРМ.РАСП(Z;0;1; ИСТИНА)
=НОРМ.СТ.РАСП(Z;ИСТИНА)
Это одинаковые формулы, только вторая формула уже создана для функции стандартного нормального распределения.
Функция нормального стандартного распределения в ExcelДавайте для примера рассмотрим две ситуации, когда предприятие имеет высокий риск банкротства и предприятие, имеющие низкий риск банкротства по probit-модели Змиевского.
Расчет probit-модели Змиевского в Excel
Для первого набора финансовых коэффициентов (-2.5, 1.5, 5) предприятие можно определить к классу банкротов. Второй набор финансовых коэффициентов (3,1,4) определяет высокую кредитоспособность предприятия, т.к. P =0 (не пугайтесь этих больших чисел, т.к. это число очень небольшое) .
Экспресс-оценка финансового состояния по модели
Оценка финансового состояния предприятия происходит аналогично модели Чессера, только без выдачи вероятности банкротства. Предприятие будет определяться в класс банкротов при P=1 и к классу финансово устойчивых при P=0.
Резюме
Итак, мы разобрали две статистические модели оценки риска банкротства предприятия (модель Чессера и модель Змиевского). Одна построена с помощью логистической регрессии, а другая с помощью пробит-регрессии. Эти две модели были пионерами в области использования нового математического аппарата для оценки финансового состояния предприятия. Использовать их можно в качестве экспресс-диагностики финансового состояния предприятия.
Спасибо за внимание! Удачи!Автор: Жданов Василий Юрьевич, к.э.н.
Моделирование в электронных таблицах
Главная | Информатика и информационно-коммуникационные технологии | Планирование уроков и материалы к урокам | 11 классы | Планирование уроков на учебный год | Моделирование в электронных таблицах
Моделирование ситуаций
ЗАДАЧА 3.4. Обои и комната
I этап. Постановка задачи
ОПИСАНИЕ ЗАДАЧИ
В магазине продаются обои. Наименования, длина и ширина рулона известны. Для удобства обслуживания надо составить таблицу, которая позволит определить необходимое количество рулонов для оклейки любой комнаты.
ЦЕЛЬ МОДЕЛИРОВАНИЯ
Помочь покупателям быстро определять необходимое количество рулонов обоев.
ФОРМАЛИЗАЦИЯ ЗАДАЧИ
Формализуем задачу в виде поиска ответов на вопросы.
II этап. Разработка модели
ИНФОРМАЦИОННАЯ МОДЕЛЬ
Дополним информационную модель в табличной форме математической моделью.
При расчете фактической площади рулона, которая пойдет на оклейку помещения, надо отбросить обрезки. Формула имеет вид:
В прямоугольной комнате две стены площадью ah и две стены площадью bh. При расчете фактической площади стен учитывается неоклеиваемая площадь окон и дверей
Необходимо также учесть, что количество рулонов должно быть целым числом, но не меньшим, чем значение N.
Количество рулонов, необходимых для оклейки комнаты, вычисляется по формуле
Примечание. Значения, указанные в исходных данных в процентах — Обр и НП, — используются в расчетных формулах в виде числа, получаемого делением процентного значения на 100. При выполнении расчетов в электронных таблицах делить на 100 не надо, так как тип данных Процент воспринимается средой именно как такое число.
КОМПЬЮТЕРНАЯ МОДЕЛЬ
Для моделирования выберем среду табличного процессора. В этой среде информационная и математическая модели объединяются в таблицу, которая содержит три области: ♦ исходные данные; ♦ промежуточные расчеты; ♦ результаты.
Заполните по образцу расчетную таблицу.
Введите формулы в расчетные ячейки.
Примечание. Функция ЦЕЛОЕ() округляет до ближайшего целого числа, меньшего, чем заданное. Но поскольку количество рулонов нельзя округлять в меньшую сторону, то к значению функции прибавляем 1 для округления в большую сторону и получаем 1 запасной рулон.
III этап. Компьютерный эксперимент
ПЛАН ЭКСПЕРИМЕНТА
ТЕСТИРОВАНИЕ
Провести тестовый расчет компьютерной модели по данным, приведенным в таблице.
ЭКСПЕРИМЕНТ 1
Провести расчет количества рулонов обоев для помещений вашей квартиры.
ЭКСПЕРИМЕНТ 2
Изменить данные некоторых образцов обоев и проследить за пересчетом результатов.
ЭКСПЕРИМЕНТ 3
Добавить строки с образцами и дополнить модель расчетом по новым образцам.
ПРОВЕДЕНИЕ ИССЛЕДОВАНИЯ
1. Введите в таблицу тестовые данные и сравните результаты тестового расчета с результатами, приведенными в таблице.
2. Поочередно введите размеры комнат вашей квартиры и результаты расчетов скопируйте в текстовый редактор.
3. Составьте отчет.
4. Проведите другие виды расчетов согласно плану.
IV этап. Анализ результатов
По данным таблицы можно определить количество рулонов каждого образца обоев для любой комнаты.
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
ЗАДАЧА 3.5.
Составить таблицу определения необходимого количества рулонов для типовых размеров комнат.
РЕКОМЕНДАЦИИ ПО РЕШЕНИЮ ЗАДАЧИ
Для построения требуемой таблицы надо воспользоваться моделью задачи 3.4. Результаты экспериментов для различных параметров комнаты копировать и вставлять на свободное пространство электронной таблицы при помощи команды Специальная вставка|Только значения. Оформить таблицу соответствующими пояснениями.
ЗАДАЧА 3.6.
Компьютерный магазин
I этап. Постановка задачи
ОПИСАНИЕ ЗАДАЧИ
Магазин компьютерных аксессуаров продает товары, указанные в прайс-листе. Стоимость указана в долларах. Если стоимость товара превышает некоторую сумму, покупателю предоставляется скидка. Составить таблицу-шаблон, позволяющую быстро рассчитать стоимость произвольной покупки. В расчете учесть текущий курс доллара.
Примечание. Прайс-лист — список товаров с ценами.
ЦЕЛЬ МОДЕЛИРОВАНИЯ
Автоматизировать расчет стоимости покупки.
Составить шаблон расчетной квитанции для покупателя.
ФОРМАЛИЗАЦИЯ ЗАДАЧИ
Проведем формализацию задачи, ответив на вопросы.
II этап. Разработка модели
ИНФОРМАЦИОННАЯ МОДЕЛЬ
Дополним информационную модель в табличной форме математической моделью.
Примечание. Значение, указанное в исходных данных в процентах — Ск, — используется в расчетных формулах в виде числа, получаемого делением процентного значения на 100. При выполнении расчетов в электронных таблицах делить на 100 не надо, так как тип данных Процент воспринимается средой именно как такое число.
КОМПЬЮТЕРНАЯ МОДЕЛЬ
Поскольку одной из целей моделирования является создание шаблона расчетной квитанции для покупателя, то в компьютерной модели надо помимо данных, необходимых для расчета, поместить информацию о названии магазина, дате покупки.
Составьте компьютерную модель по приведенному образцу.
Введите в ячейки исходные данные, расчетные формулы.
III этап. Компьютерный эксперимент
ПЛАН ЭКСПЕРИМЕНТА
ТЕСТИРОВАНИЕ
Провести тестовый расчет компьютерной модели по данным, приведенным в таблице.
ЭКСПЕРИМЕНТ 1
Ввести курс доллара на текущий день, размер скидки и провести расчет покупки со своим количеством товара.
ЭКСПЕРИМЕНТ 2
Добавить строки другими видами товаров и дополнить модель расчетом по этим данным.
ПРОВЕДЕНИЕ ИССЛЕДОВАНИЯ
1. Введите в таблицу тестовые данные и сравните результаты тестового расчета с результатами, приведенными в таблице.
2. Подберите тестовый набор исходных данных, чтобы получить сумму со скидкой.
3. Введите свои исходные данные и проследите за перерасчетом.
4. Проведите другие виды расчетов согласно плану.
IV этап. Анализ результатов моделирования
Полученная модель позволяет автоматически пересчитывать стоимость покупки с любым количеством товара из представленного ассортимента и заполнять расчетную квитанцию.
ЗАДАЧА 3.7. Сберкасса
I этап. Постановка задачи
ОПИСАНИЕ ЗАДАЧИ
За два часа до обеденного перерыва 40 бабушек встали в очередь за пенсией. Кассирша обслуживает клиента в среднем одну минуту.
Первая бабушка «мучила» кассиршу вопросами 9 мин 15 с. Каждая следующая бабушка, частично «мотая на ус» ответы, адресованные предыдущим бабушкам, «мучает» кассиршу на 10 с меньше.
Построить модель ситуации и исследовать ее.
ЦЕЛЬ МОДЕЛИРОВАНИЯ
Цель моделирования учебная: исследовать ситуацию с разных углов зрения (задания типа «что будет, если...», «как сделать, чтобы...»), сделать выводы и дать свои рекомендации по улучшению обслуживания.
ФОРМАЛИЗАЦИЯ ЗАДАЧИ
Чтобы понять суть задачи, ответим на уточняющие вопросы.
II этап. Разработка модели
ИНФОРМАЦИОННАЯ МОДЕЛЬ
Объектом моделирования является система, состоящая из кассира и очереди. Очередь тоже может быть разбита на простые элементы и представляет собой множество из 40 бабушек. Каждый из объектов, входящих в систему, имеет свои параметры. Связи между элементами системы можно схематично изобразить так.
Информационную модель в виде схемы и таблицы дополняет математическая модель ситуации, представленная следующими выражениями.
КОМПЬЮТЕРНАЯ МОДЕЛЬ
Объединим информационную и математическую модели, воспользовавшись средой табличного процессора. Для этой задачи промежуточные данные и результаты представляются в виде единого блока, так как в этом блоке содержится вся необходимая информация для анализа и выводов.
Примечание. В операциях участвуют данные типа Время. Результат выполнения такой операции будет записан в ячейке в числовой форме. Чтобы перевести числовой результат в тип Время, следует использовать опцию Тип данных меню Формат и изменить формат ячейки перед заполнением вниз.
Заполнить таблицу исходными данными. Ввести в таблицу результатов формулы для расчетов.
III этап. Компьютерный эксперимент
ПЛАН ЭКСПЕРИМЕНТА
ТЕСТИРОВАНИЕ
Проверить правильность ввода формул. Произвести расчеты.
ЭКСПЕРИМЕНТ
Изменяя значения ячеек В5, В7, В8, исследовать влияние этих характеристик на скорость движения очереди.
ПРОВЕДЕНИЕ ИССЛЕДОВАНИЯ
1. Введите в таблицу контрольные исходные данные и скопируйте расчетные формулы в две-три строки. Результаты сравните с приведенными в таблице.
Сравнение с контрольным образцом показывает правильность введения формул. Это самая простая форма тестирования.
2. Заполните формулами ячейки на 40 строк.
3. Определите по таблице (столбец С), сколько времени понадобится кассиру, чтобы обслужить всю очередь.
4. Найдите в таблице строку, которая соответствует наступлению обеденного перерыва.
IV этап. Анализ результатов моделирования
По результатам моделирования в электронных таблицах ответить на следующие вопросы:
1. Как долго будет «мучить» кассиршу сороковая бабушка?
2. Хватит ли на обслуживание всех бабушек дообеденного времени (2 часа)?
3. Если не хватит, то какую по счету бабушку успеют обслужить до перерыва?
4. Хватит ли времени на обслуживание всей очереди до конца рабочего дня, если после перерыва касса будет открыта еще 4 часа?
5. Как влияет на время обслуживания очереди уменьшение Ткл? Можно ли сильно уменьшить Ткл и к чему это приведет?
6. Как влияет на время обслуживания очереди уменьшение времени расспросов? Можно ли сокращать это время и к чему это приведет?
7. Какие из предыдущих вопросов можно отнести к задаче типа: «что будет, если...», а какие — к задаче «как сделать, чтобы...»?
8. Сформулировать рекомендации символическому кассиру и бабушкам по организации процесса обслуживания. Например, стоит ли выделить отдельного сотрудника, который будет разъяснять возникающие вопросы? Какие другие способы информирования можно использовать? Сколько сотрудников должны работать в кассе, чтобы обслужить клиентов до обеда?
9. Оформить результаты в виде отчета в текстовом процессоре.
ЗАДАЧА 3.8. Нерадивый ученик
I этап. Постановка задачи
ОПИСАНИЕ ЗАДАЧИ
Мальчик учит стихотворение из 40 строк. Чтобы запомнить первую строчку, ему понадобилась всего 1 мин. На каждую следующую он тратит на 10% времени больше. Стихотворение держится в памяти нерадивого ученика не дольше 3 часов, а до школы бежать 15 мин. Как организовать заучивание стихотворения?
ЦЕЛЬ МОДЕЛИРОВАНИЯ
Предлагается исследовать ситуацию и предложить реальные способы ускорения процесса заучивания стихотворения.
ФОРМАЛИЗАЦИЯ ЗАДАЧИ
Ответим на уточняющие вопросы по условию задачи.
II этап. Разработка модели
ИНФОРМАЦИОННАЯ МОДЕЛЬ
Анализ объекта моделирования показывает, что эта система состоит из двух объектов: мальчика и стихотворения. Стихотворение, в свою очередь, может быть разбито на простые элементы — строки. Каждый из объектов, входящих в систему, имеет свои параметры. Связь между объектами этой системы заключается во времени заучивания стиха нерадивым учеником.
Схема связей между элементами системы достаточно проста.
КОМПЬЮТЕРНАЯ МОДЕЛЬ
Объединим информационную и математическую модели, воспользовавшись средой табличного процессора. Для этой задачи промежуточные данные и результаты представляют собой единый блок, в котором содержится вся необходимая информация для анализа и выводов. Заполнить таблицу исходными данными по приведенному образцу.
Примечание. Заполняя в таблице исходные данные, обратите внимание, что значение в ячейку В5 вводится по формату Время, а в ячейку В6 — по формату Процент (число со знаком %). При вводе в ячейку значения в формате Процент в самой ячейке записана процентная форма данного, а в строке состояния высвечивается числовая форма данного.
Ввести формулы для расчетов:
III этап. Компьютерный эксперимент
ПЛАН ЭКСПЕРИМЕНТА
ТЕСТИРОВАНИЕ
Проверить правильность ввода формул.
ЭКСПЕРИМЕНТ 1
Рассчитать в электронных таблицах время заучивания каждой строки стихотворения и суммарное время заучивания. Исследовать полученные результаты.
ЭКСПЕРИМЕНТ 2
Изменяя значения ячеек В5 и В6, исследовать влияние старательности ученика на общее время заучивания стихотворения.
ПРОВЕДЕНИЕ ИССЛЕДОВАНИЯ
ТЕСТИРОВАНИЕ
Сравнение с контрольным образцом показывает правильность ввода формул.
Ввести в таблицу контрольные исходные данные и скопировать расчетные формулы в две-три строки. Результаты сравнить с приведенными в таблице.
ЭКСПЕРИМЕНТ 1
Исследование процесса заучивания стихотворения
Скопируйте формулы в нижестоящие ячейки, в общей сложности на 40 строк.
По расчетным данным дайте ответ на следующие вопросы:
1. Сколько времени понадобилось бы мальчику, чтобы выучить все стихотворение?
2. Из скольких строк (максимум) должно состоять стихотворение, если учительница мальчика утверждает, что его знаний хватает не более чем на 3 часа, а до школы бежать 15 мин? Каким по счету может быть урок литературы, чтобы знания «не выветрились» из головы?
3. Сколько строк можно успеть выучить до начала «мультика», если до него осталось 45 мин?
ЭКСПЕРИМЕНТ 2
Исследование влияния старательности на время заучивания стихотворения
Изменяя значения ячеек В5 и В6 в реальных пределах, исследовать их влияние на время заучивания стихотворения.
По расчетным данным дайте ответ на следующие вопросы:
1. Как влияет время заучивания 1-й строки на общее время запоминания стихотворения?
2. Как влияет концентрация внимания (уменьшение D%) на общее время запоминания стихотворения?
IV этап. Анализ результатов моделирования
По результатам, рассчитанным в электронных таблицах, ответить на следующие вопросы:
1. Что нужно изменить в модели заучивания стихов, чтобы просчитать ее для любых других усидчивых и нерадивых учеников? На какой части таблицы это отразится?
2. Что нужно изменить в модели заучивания стихов, чтобы просчитать ее для стихотворения любой длины?
3. Какие из заданных в ходе эксперимента вопросов можно отнести к задаче типа «что будет, если...», а какие — к задаче типа «как сделать, чтобы...»?
4. Предложить реальные способы ускорения процесса заучивания стихотворения.
ЗАДАЧА 3.9*. Расчет кривой падения электрика
(* Задача повышенной сложности)
I этап. Постановка задачи
ОПИСАНИЕ ЗАДАЧИ
Электрик Петров приставил к стене лестницу и, поднявшись вверх, остановился на одной из ступенек. В это время концы лестницы начали скользить вдоль стены и пола. Провести исследование, по какой кривой будет падать вниз электрик Петров.
ЦЕЛИ МОДЕЛИРОВАНИЯ
Исследовать движение лестницы.
ФОРМАЛИЗАЦИЯ ЗАДАЧИ
Проведем формализацию задачи в виде поиска ответов на вопросы.
Будем считать, что лестница первоначально занимала вертикальное положение. Это не совсем реально, но удобно для дальнейших расчетов.
II этап. Разработка модели
ИНФОРМАЦИОННАЯ МОДЕЛЬ
Результаты формализации задачи сведем в таблицу.
Для построения математической модели воспользуемся чертежом. Так как верхний конец А скользит вдоль стены, то у него изменяется только координата у от L до 0, а координата х всегда равна 0, а для конца В, наоборот, — х изменяется от 0 до L, у = 0. У промежуточных точек изменяются обе координаты.
Вычислим координаты ступеньки с номером k, которая располагается в точке С.
КОМПЬЮТЕРНАЯ МОДЕЛЬ
Для построения компьютерной модели выберем среду табличного процессора. В ней табличная информационная и математическая модели объединяются в таблицу, которая содержит три области:
♦ исходные данные; ♦ промежуточные расчеты; ♦ результаты.
Заполните таблицу по представленному образцу.
Примечание. При использовании встроенных функций SIN() и COS() важно помнить, что угол должен быть выражен в радианах. Введите в расчетные ячейки формулы:
Пример заполнения электронной таблицы.
III этап. Компьютерный эксперимент
ПЛАН ЭКСПЕРИМЕНТА
ТЕСТИРОВАНИЕ
Проверить правильность ввода формул.
ЭКСПЕРИМЕНТ
1. Исследовать вид кривой падения электрика в зависимости от номера ступеньки.
2. Исследовать вид кривой в зависимости от номера ступеньки. ПРОВЕДЕНИЕ ИССЛЕДОВАНИЯ
ТЕСТИРОВАНИЕ
1. Сравните результаты, полученные после ввода формул, с результатами, приведенными в примере расчета. Совпадение значений с контрольным образцом показывает правильность введения формул.
2. По столбцам С и D постройте диаграмму кривой, по которой движется ступенька с электриком.
ЭКСПЕРИМЕНТ. Исследование вида кривой
Постройте диаграммы кривых для различных номеров ступенек и скопируйте их в текстовый документ. Для этого:
♦ Введите в ячейку Сб номер ступеньки. Проследите за пересчетом значений в таблице и изменениями на диаграмме. ♦ Уравняйте масштабы по осям Ох и Оу. Это очень важно, чтобы потом можно было сравнивать виды кривых. ♦ Скопируйте диаграмму в текстовый документ. ♦ Повторите действия для других номеров ступенек.
IV этап. Анализ результатов моделирования
1. Просмотрите диаграммы кривых различных номеров ступенек.
2. Убедитесь, что кривая похожа на четверть эллипса, сплющенного или к оси ординат (если номер ступеньки больше 5), или к оси абсцисс (если номер ступеньки меньше 5). А на что похожа кривая, если номер ступеньки, на которой стоит электрик, равен 5?
3. Сформулируйте и запишите выводы по результатам исследования в текстовый документ.
ЗАДАЧА 3.10*. Дачник и собака
* Задача повышенной сложности.
I этап. ПОСТАНОВКА ЗАДАЧИ
ОПИСАНИЕ ЗАДАЧИ
От железнодорожной станции по направлению к дачному поселку движется пешеход. Одновременно с ним в том же направлении бежит собака. Поскольку собака бежит быстрее, то, добежав до дома и радостно известив о приближении хозяина, она разворачивается и бежит к человеку, а от него обратно к дому...
Какой суммарный путь пробежит собака за время, пока человек дойдет до дома?
ЦЕЛЬ МОДЕЛИРОВАНИЯ
Исследовать процесс движения объектов: человека и собаки. Установить связь между расстояниями, пройденными объектами за одно и то же время. Определить путь, который пробежала собака.
ФОРМАЛИЗАЦИЯ ЗАДАЧИ
Проведем формализацию задачи в виде поиска ответов на следующие вопросы.
II этап. Разработка модели
ИНФОРМАЦИОННАЯ МОДЕЛЬ
На рисунке 3.1 представлены объекты и параметры системы. Рисунок позволяет наглядно представить процесс движения.
Составим математическую модель, связывающую параметры движения системы.
Рассмотрим два отрезка движения:
♦ собака бежит от человека к даче; ♦ собака бежит от дачи к человеку (первая встреча).
Параметры движения собаки от человека к даче определяются по формулам:
Параметры движения собаки от дачи к человеку до их первой встречи определяются по формуле:
Эта формула получается следующим образом. Расстояние, которое было между человеком и собакой, когда они начинают двигаться навстречу друг другу, равно Sд1 - Рд1. Оно также может быть представлено как сумма расстояний, пройденных каждым участником до встречи Vc х tч1 + Vч1 х tч1. Поскольку собака и человек движутся навстречу друг другу, то время движения до встречи у них одинаковое. Но так как скорости разные, то расстояния, которые они пройдут, тоже разные. Приравняем эти выражения:
Будем строить модель пути, пройденного собакой, как сумму отрезков, которые она пробегает от человека до дачи и обратно. Обозначим их S1, S2, S3,... Путь, пройденный собакой от момента расставания с человеком у станции до новой встречи с ним: S1 = Sд1 + Sч1.
КОМПЬЮТЕРНАЯ МОДЕЛЬ
Для построения компьютерной модели выбираем среду табличного процессора, которая содержит три области:
♦ исходные данные; ♦ промежуточные расчеты; ♦ результаты.
1. Заполните область исходных данных по образцу.
2. Для суммирования в результирующем столбце G отрезков пути, пройденных собакой, в ячейку G9 введите 0 (ноль) — путь, пройденный собакой в начальный момент времени.
3. Заполните расчетные ячейки по формулам:
III этап. Компьютерный эксперимент
ПЛАН ЭКСПЕРИМЕНТА
ТЕСТИРОВАНИЕ
Провести тестовый расчет компьютерной модели.
ЭКСПЕРИМЕНТ
Провести расчеты с различными исходными значениями скоростей объектов и расстояния между станцией и дачей.
ПРОВЕДЕНИЕ ИССЛЕДОВАНИЯ
1. Введите в таблицу тестовые данные и сравните результаты тестового расчета с результатами, приведенными ниже.
2. Измените скорость человека и проследите, как это отразится на результатах.
3. Измените расстояние между пунктами.
4. Измените скорость собаки.
IV этап. Анализ результатов моделирования
Ответить на вопрос, поставленный в задаче. Оформить выводы и результаты расчетов в текстовом редакторе.
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
3.11. Продукты для похода.
Для организации похода надо построить модель расчета нормы продуктов для группы туристов. Известна норма каждого продукта на 1 человека на 1 день, количество человек и количество дней похода.
Рассчитать необходимое количество продуктов на весь поход для 1 человека и для всей группы. Провести расчеты для разных исходных значений количества дней и туристов. Нормы продуктов приведены в таблице.
3.12. Концентрация раствора.
В магазине продается 70%-ный раствор уксусной эссенции. Для домашних нужд обычно используется раствор меньшей концентрации и в разных количествах. Примеры приведены в таблице. Составьте таблицу, по которой можно определить, как изменяется исходная концентрация при добавлении 1, 2, 3 и т. д. частей воды. По таблице определите, сколько надо взять частей воды на 1 часть уксусной эссенции, чтобы получить нужное количество раствора требуемой концентрации, а также подберите вес исходной части раствора (и воды), чтобы получить требуемое количество разбавленного раствора. Исходными данными являются:
• исходная концентрация раствора; • вес 1 части раствора исходной концентрации (и 1 части воды).
3.13. Буратино и папа Карло.
У папы Карло было накоплено 20 золотых, когда Буратино поступил на работу в кукольный театр Карабаса Барабаса. Еженедельно Буратино приносит зарплату 5 золотых, а папа Карло тратит половину (50%) имеющегося на начало недели богатства. Постройте модель изменения капитала в течение нескольких недель. Исследуйте модель и ответьте на вопросы:
1. Как изменяется капитал, если увеличить (уменьшить) начальный капитал папы Карло? 2. Как изменяется капитал, если увеличить (уменьшить) зарплату Буратино? 3. Как изменяется капитал, если увеличить (уменьшить) процент еженедельной траты капитала?
3.14. Расписание движения автобуса.
Маршрут автобуса включает 8 остановок. Время движения между остановками задано массивом. Составить расписание движения автобуса в течение рабочего дня, учитывая следующие условия:
• время работы маршрута 5:30-24:00; • частота движения автобуса на маршруте зависит от времени дня и составляет в часы «пик» с 6:30 до 8:30 и с 17:30 до 19:00 — 7 мин; в остальное время дня — 15 мин.
3.15. График тренировки.
Начав тренировки, спортсмен в первый день пробежал 10 км. Каждый следующий день он пробегал на 10% больше предыдущего. Построить таблицу «График тренировок», в которой имеются следующие столбцы:
По таблице определить:
1. Суммарный пробег за 7 дней. 2. Через сколько дней спортсмен будет пробегать в день более 20 км. 3. Через сколько дней суммарный пробег превысит 100 км.
3.16. Аквариум.
Мальчик решил почистить аквариум. Начал с переселения рыбок в банку. Семейство рыбок, проживающих в аквариуме, составляло 40 штук. Первую рыбку он поймал быстро, затратив 5 с, и еще 2 с потратил на перекладывание в банку. Но чем меньше становилось в воде рыбок, тем труднее было их поймать. На каждую следующую рыбку он затрачивал времени больше на 5%, чем на предыдущую.
Сколько минут он затратит на переселение рыбок?
3.17. Награда.
Шахматы были изобретены в Индии. Индусский царь Шерам решил наградить изобретателя шахмат, вызвал его к себе и сказал, что исполнит любую его просьбу. Изобретатель удивил царя беспримерной скромностью просьбы:
— Прикажи выдать мне за первую клетку шахматной доски 1 пшеничное зерно, за вторую — 2, за каждую следующую в два раза больше, чем за предыдущую.
Сколько килограммов зерен было выдано изобретателю, если 1 зерно весит 0,05 г?
- Шины континенталь зимние официальный сайт

- Компрессор для автомобиля для колес

- Pirelli cinturato p6 отзывы

- Производитель резина бриджстоун

- Чье производство бриджстоун

- На гольф диски

- Отзывы кама нф 202

- Разболтовка вольво s40

- Размер шин мазда 6 gh

- Тест зимних шин за рулем р14

- 124 мерседес диски


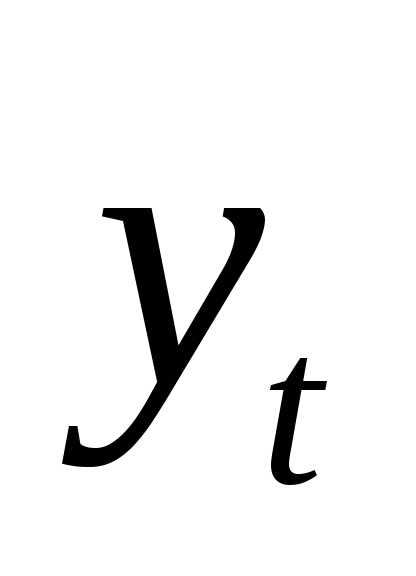
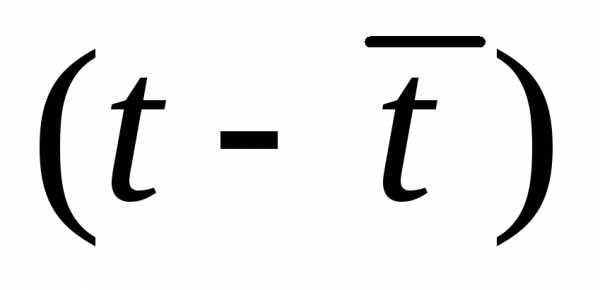
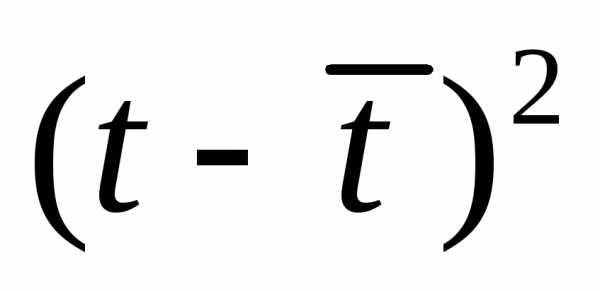
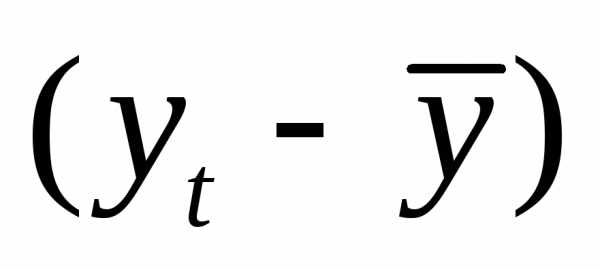

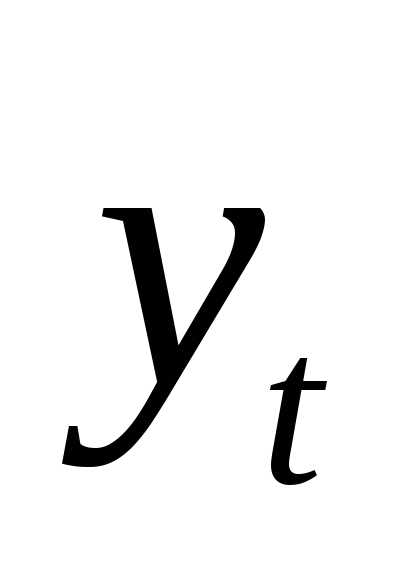
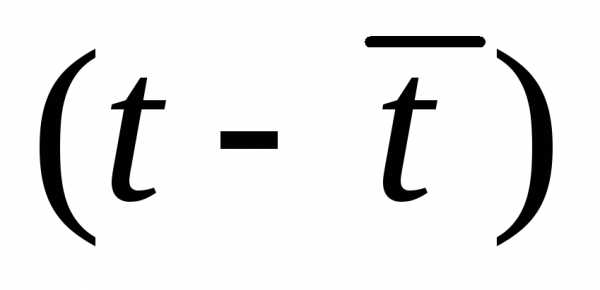
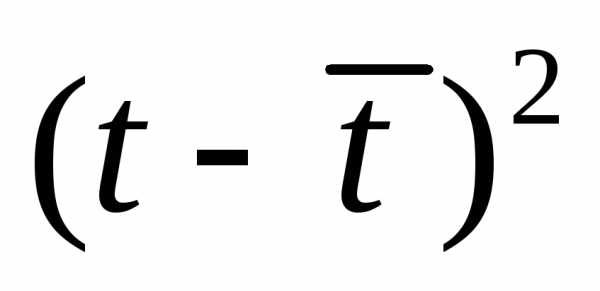
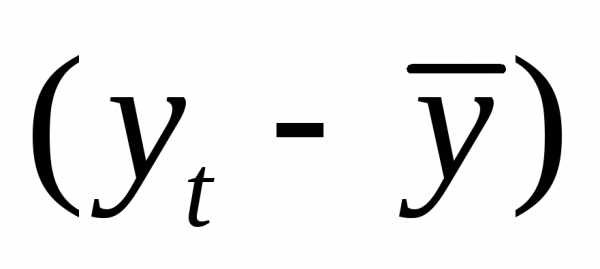
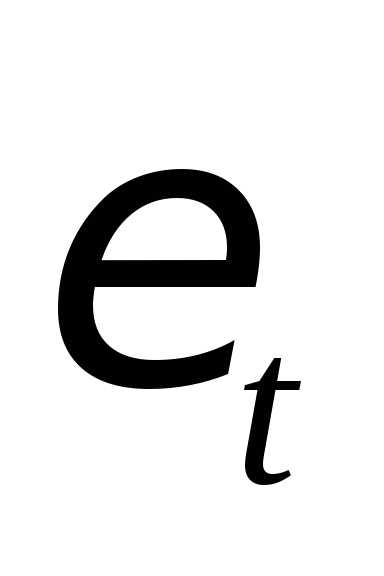
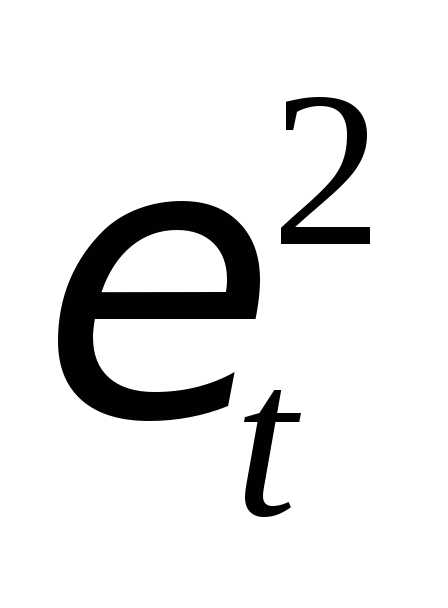
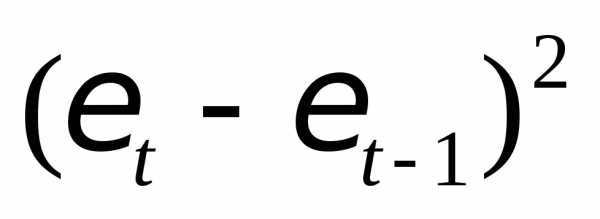
 = 0 ?
= 0 ?